题目内容
10.已知函数f(x)=x2+3x+a(1)当a=-2时,求不等式f(x)>2的解集
(2)若对任意的x∈[1,+∞),f(x)>0恒成立,求实数a的取值范围.
分析 (1)直接利用二次不等式转化求解即可.
(2)利用函数恒成立,分离变量,利用函数的最值求解即可.
解答 解:(1)当a=-2时,不等式f(x)>2可化为x2+3x-4>0,
解得{x|x<-4或x>1} …(5分)
(2)若对任意的x∈[1,+∞),f(x)>0恒成立,
则a>-x2-3x在x∈[1,+∞)恒成立,
设g(x)=-x2-3x
则g(x)在区间x∈[1,+∞)上为减函数,当x=1时g(x)取最大值为-4,
∴a得取值范围为{a|a>-4} …(10分).
点评 本题考查二次函数的性质,函数恒成立条件的应用,二次不等式的解法,考查转化思想以及计算能力.

练习册系列答案
相关题目
18.某几何体的三视图如图所示,其中俯视图中半圆半径为$\sqrt{2}$,则该几何体的体积是( )
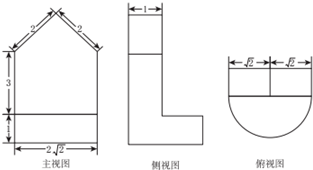

| A. | $2π+8\sqrt{2}+2$ | B. | $2π+8\sqrt{2}+1$ | C. | $π+8\sqrt{2}+1$ | D. | $π+8\sqrt{2}+2$ |
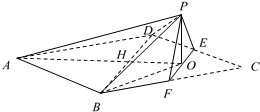 边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.
边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.