题目内容
(本题满分15分)函数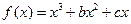 在
在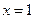 处取得极小值–2.(I)求
处取得极小值–2.(I)求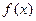 的单调区间;(II)若对任意的
的单调区间;(II)若对任意的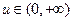 ,函数
,函数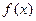 的图像
的图像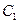 与函数
与函数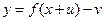 的图像
的图像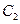 至多有一个交点.求实数
至多有一个交点.求实数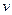 的范围.
的范围.
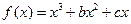 在
在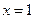 处取得极小值–2.(I)求
处取得极小值–2.(I)求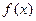 的单调区间;(II)若对任意的
的单调区间;(II)若对任意的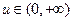 ,函数
,函数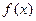 的图像
的图像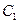 与函数
与函数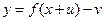 的图像
的图像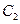 至多有一个交点.求实数
至多有一个交点.求实数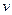 的范围.
的范围.(Ⅰ) 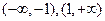 是单调递增区间,
是单调递增区间,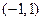 是单调递减区间. (Ⅱ)
是单调递减区间. (Ⅱ) 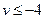 …
…
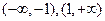 是单调递增区间,
是单调递增区间,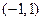 是单调递减区间. (Ⅱ)
是单调递减区间. (Ⅱ) 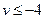 …
…(I)
 ,
,
由题意得: 解得
解得
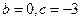 …………………………………………4 分
…………………………………………4 分
∴
∴当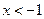 或
或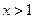 时
时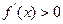 ;当
;当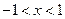 时
时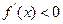
∴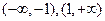 是单调递增区间,
是单调递增区间,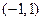 是单调递减区间.…………………………………7 分
是单调递减区间.…………………………………7 分
(II)
由方程组
得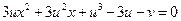 至多有一个实根………………………………………………9 分
至多有一个实根………………………………………………9 分
∴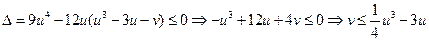 恒成立……………12 分
恒成立……………12 分
 令
令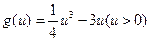 ,则
,则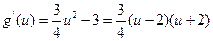 由此知函数
由此知函数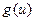 在(0,2)上为减函数,在
在(0,2)上为减函数,在 上为增函数,
上为增函数,
所以当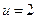 时,函数
时,函数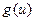 取最小值,即为
取最小值,即为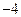 ,于是
,于是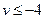 ………………………………15 分
………………………………15 分

 ,
,由题意得:
 解得
解得
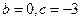 …………………………………………4 分
…………………………………………4 分∴

∴当
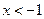 或
或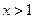 时
时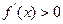 ;当
;当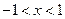 时
时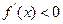
∴
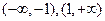 是单调递增区间,
是单调递增区间,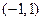 是单调递减区间.…………………………………7 分
是单调递减区间.…………………………………7 分(II)

由方程组

得
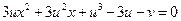 至多有一个实根………………………………………………9 分
至多有一个实根………………………………………………9 分∴
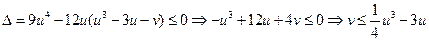 恒成立……………12 分
恒成立……………12 分 令
令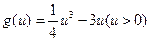 ,则
,则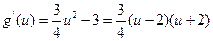 由此知函数
由此知函数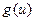 在(0,2)上为减函数,在
在(0,2)上为减函数,在 上为增函数,
上为增函数,所以当
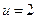 时,函数
时,函数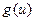 取最小值,即为
取最小值,即为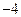 ,于是
,于是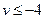 ………………………………15 分
………………………………15 分
练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
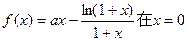 处取得极值.
处取得极值.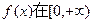 上的单调性;
上的单调性;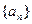 满足
满足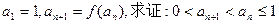 ;
;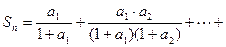
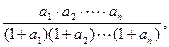
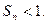
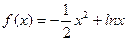 ,
,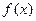 的单调区间;
的单调区间;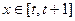
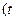 为大于0的常数),求
为大于0的常数),求 在y轴上的截距是2,且在
在y轴上的截距是2,且在 上单调递增,在(-1,2)上单调递减.
上单调递增,在(-1,2)上单调递减. ,求
,求 的单调区间.
的单调区间.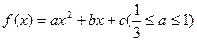 的图象经过A(0,1),且在该点处的切线与直线
的图象经过A(0,1),且在该点处的切线与直线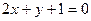 平行.
平行.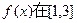 上的最大值与最小值分别为M(a),N(a),求F(a)=M(a)-N(a)的表达式.
上的最大值与最小值分别为M(a),N(a),求F(a)=M(a)-N(a)的表达式.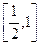 上变化时,证明:
上变化时,证明: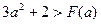
 构成的集合:
构成的集合: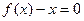 有实根;②函数
有实根;②函数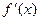 满足0<
满足0<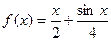 ,判断方程
,判断方程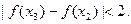
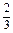 .
.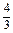 .
.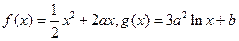 ,其中
,其中 。设两曲线
。设两曲线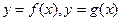 有公共点,且在公共点处的切线相同。
有公共点,且在公共点处的切线相同。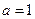 ,求
,求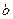 的值;
的值;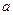 表示
表示
 ,求
,求 .
.