题目内容
已知函数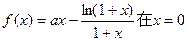 处取得极值.
处取得极值.
(1)求实数a的值,并判断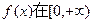 上的单调性;
上的单调性;
(2)若数列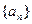 满足
满足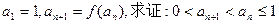 ;
;
(3)在(2)的条件下,
记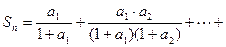
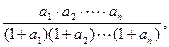
求证: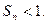
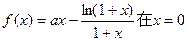 处取得极值.
处取得极值.(1)求实数a的值,并判断
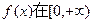 上的单调性;
上的单调性;(2)若数列
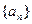 满足
满足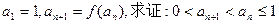 ;
;(3)在(2)的条件下,
记
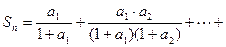
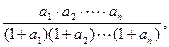
求证:
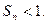
(1)1 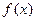 在
在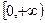 上是增函数.(2)见解析(3)见解析
上是增函数.(2)见解析(3)见解析
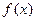 在
在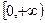 上是增函数.(2)见解析(3)见解析
上是增函数.(2)见解析(3)见解析(1)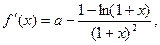
由题知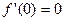 ,即a-1=0,∴a=1.
,即a-1=0,∴a=1.
则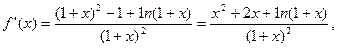
∵x≥0,∴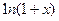 ≥0,
≥0,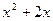 ≥0,又∵
≥0,又∵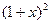 >0,∴x≥0时,
>0,∴x≥0时,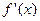 ≥0,
≥0,
∴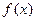 在
在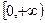 上是增函数.
上是增函数.
(Ⅱ)由(Ⅰ)知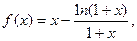 ∴
∴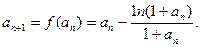
下面用数学归纳法证明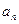 >0.①当n=1时,
>0.①当n=1时,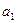 =1>0成立;
=1>0成立;
②假设当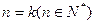 时,
时,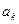 >0,∵
>0,∵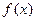 在
在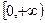 上是增函数,
上是增函数,
∴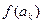 >
>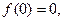 ∴
∴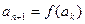 >0成立,综上当
>0成立,综上当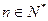 时,
时,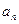 >0.
>0.
又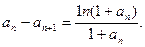 ∵
∵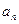 >0,1+
>0,1+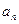 >1,∴
>1,∴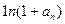 >0,∵
>0,∵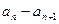 >0,
>0,
∴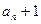 <
<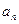 ,
,
而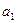 =1,∴
=1,∴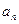 ≤1,综上,0<
≤1,综上,0<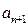 ≤1.(3)∵0<
≤1.(3)∵0<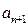 <
<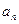 ≤1,
≤1,
∴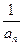 <
<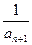 ,∴
,∴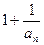 <
<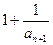 ,∴
,∴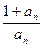 <
<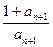 ,
,
∴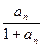 >
>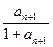 >0,
>0,
∴ =
=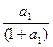 ·
·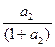 …
…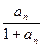 <
<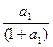 ·
·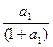 ……
…… 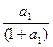 =
=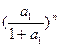 n.
n.
∴Sn=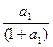 +
+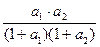 +…+
+…+
<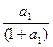 +(
+(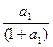 )2+…+(
)2+…+(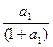 )n
)n
=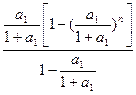 <
<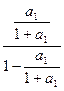 =
=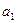 =1.
=1.
∴Sn<1.
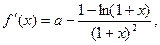
由题知
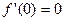 ,即a-1=0,∴a=1.
,即a-1=0,∴a=1.则
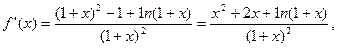
∵x≥0,∴
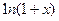 ≥0,
≥0,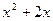 ≥0,又∵
≥0,又∵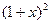 >0,∴x≥0时,
>0,∴x≥0时,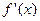 ≥0,
≥0,∴
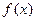 在
在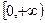 上是增函数.
上是增函数. (Ⅱ)由(Ⅰ)知
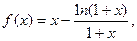 ∴
∴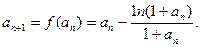
下面用数学归纳法证明
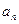 >0.①当n=1时,
>0.①当n=1时,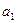 =1>0成立;
=1>0成立;②假设当
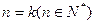 时,
时,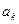 >0,∵
>0,∵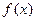 在
在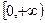 上是增函数,
上是增函数,∴
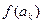 >
>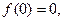 ∴
∴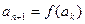 >0成立,综上当
>0成立,综上当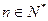 时,
时,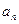 >0.
>0.又
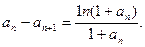 ∵
∵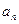 >0,1+
>0,1+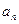 >1,∴
>1,∴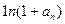 >0,∵
>0,∵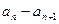 >0,
>0,∴
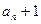 <
<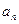 ,
,而
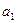 =1,∴
=1,∴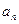 ≤1,综上,0<
≤1,综上,0<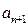 ≤1.(3)∵0<
≤1.(3)∵0<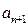 <
<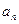 ≤1,
≤1,∴
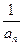 <
<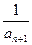 ,∴
,∴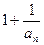 <
<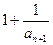 ,∴
,∴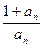 <
<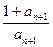 ,
,∴
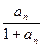 >
>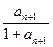 >0,
>0,∴
 =
=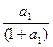 ·
·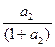 …
…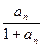 <
<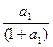 ·
·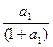 ……
…… 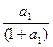 =
=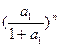 n.
n.∴Sn=
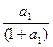 +
+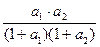 +…+
+…+
<
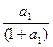 +(
+(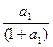 )2+…+(
)2+…+(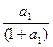 )n
)n=
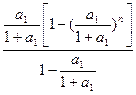 <
<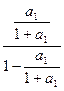 =
=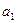 =1.
=1.∴Sn<1.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
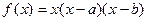 ,点A(s,f(s)), B(t,f(t))
,点A(s,f(s)), B(t,f(t))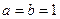 ,求函数
,求函数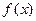 的单调递增区间;
的单调递增区间; 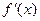 满足:当|x|≤1时,有|
满足:当|x|≤1时,有|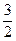 恒成立,求函数
恒成立,求函数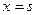 和
和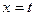 处取得极值,且
处取得极值,且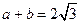 ,证明:
,证明: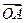 与
与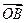 不可能垂直.
不可能垂直.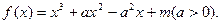
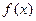 在
在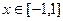 内没有极值点,求
内没有极值点,求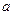 的取值范围。
的取值范围。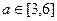 ,不等式
,不等式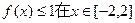 上恒成立,求实数
上恒成立,求实数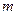 的取值范围。
的取值范围。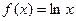 ,
,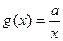 ,设
,设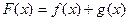 .
.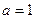 时,求函数
时,求函数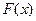 的单调区间;
的单调区间;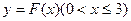 图象上任意一点
图象上任意一点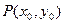 为切点的切线斜率
为切点的切线斜率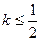 恒成立,求实数
恒成立,求实数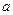 的最小值.
的最小值. 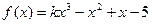 在R上单调递增,记
在R上单调递增,记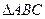 的三内角
的三内角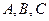 的对应边分别为
的对应边分别为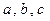 ,若
,若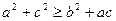 时,不等式
时,不等式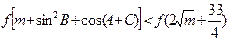 恒成立.
恒成立.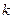 的取值范围;
的取值范围;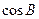 的取值范围;
的取值范围;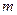 的取值范围.
的取值范围.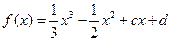 有极值.
有极值.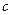 的取值范围;
的取值范围;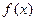 在
在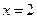 处取得极值,且当
处取得极值,且当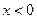 时,
时,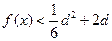 恒成立,求
恒成立,求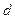 的取值范围.
的取值范围.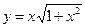 ;
;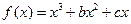 在
在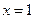 处取得极小值–2.(I)求
处取得极小值–2.(I)求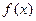 的单调区间;(II)若对任意的
的单调区间;(II)若对任意的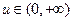 ,函数
,函数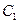 与函数
与函数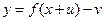 的图像
的图像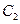 至多有一个交点.求实数
至多有一个交点.求实数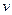 的范围.
的范围.