题目内容
直线y=kx+k与圆x2+y2=1位置关系是 .
考点:直线与圆的位置关系
专题:计算题,直线与圆
分析:判断直线恒过的定点与圆的位置关系,即可得到结论.
解答:
解:因为直线y=kx+k恒过(-1,0)且斜率存在,而点(-1,0)在圆x2+y2=1上,
所以直线与圆的位置关系是相交.
故答案为:相交.
所以直线与圆的位置关系是相交.
故答案为:相交.
点评:本题考查直线与圆的位置关系,考查计算能力,比较基础.

练习册系列答案
相关题目
双曲线
-
=1的焦点坐标是( )
| x2 |
| 36 |
| y2 |
| 64 |
| A、(0,-10),(0,10) | ||||
| B、(-10,0),(10,0) | ||||
C、(-2
| ||||
D、(0,-2
|
设函数f1(x)=x,f2(x)=log2014x,f3(x)=
,ai=
i=1,2,…,2015,记Ik=|fk(a2)-fk(a1)|+|fk(a3)-fk(a2)|+…+|fk(a2015)-fk(a2014)|,k=1,2,3 则( )
| 1 |
| x |
| i |
| 2015 |
| A、I1<I3<I2 |
| B、I1<I2<I3 |
| C、I2<I1<I3 |
| D、I3<I2<I1 |
以(2,0)为圆心,经过原点的圆方程为( )
| A、(x+2)2+y2=4 |
| B、(x-2)2+y2=4 |
| C、(x+2)2+y2=2 |
| D、(x-2)2+y2=2 |
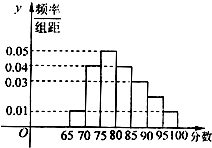 如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人.
如图为某校语言类专业N名毕业生的综合测评成绩(百分制)分布直方图,已知80~90分数段的学员数为21人.