题目内容
若正实数x，y满足x+y+1=xy，则x+2y的最小值是（ ）
| A、3 | B、5 | C、7 | D、8 |
考点：基本不等式
专题：不等式的解法及应用
分析：由已知正实数x，y满足x+y+1=xy，可得y＞1，x=
．代入x+2y变形利用基本不等式即可得出．
| y+1 |
| y-1 |
解答：
解：∵正实数x，y满足x+y+1=xy，
∴y＞1，x=
．
∴x+2y=
+2y=1+
+2(y-1)+2≥1+2×2
+2=7，当且仅当y=2时取等号．
故选：C．
∴y＞1，x=
| y+1 |
| y-1 |
∴x+2y=
| y+1 |
| y-1 |
| 2 |
| y-1 |
|
故选：C．
点评：本题考查了变形利用基本不等式，属于基础题．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
如图，函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0，|φ|≤下列函数中，以
为最小正周期的是（ ）
| π |
| 2 |
A、y=sin
| ||
| B、y=sinx | ||
| C、y=sin2x | ||
| D、y=sin4x |
如图给出的计算1+
+
+…+
的值的一个程序框图，则判断框内应填入的条件是（ ）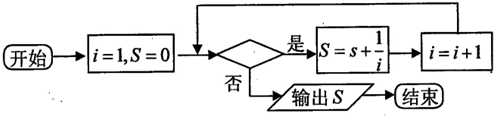
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2014 |
| A、i≤2014 |
| B、i＞2014 |
| C、i≤2013 |
| D、i＞2013 |
二项式（2x+
）6展开式中的常数项是（ ）
| 1 | ||
|
| A、15 | B、60 |
| C、120 | D、240 |
抛物线y=2（x+1）2-3的顶点坐标是（ ）
| A、（1，3） |
| B、（-1，3） |
| C、（1，-3） |
| D、（-1，-3） |
从5名医生（3男2女）中随机等可能地选派两名医生，则恰选得一名男医生和一名女医生的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|