题目内容
5.在△ABC中,a=2,b=$\sqrt{2}$,∠A=$\frac{π}{4}$,则∠B=( )| A. | 30° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
分析 由已知利用正弦定理可求sinB的值,结合大边对大角可得B为锐角,从而得解.
解答 解:在△ABC中,∵a=2,b=$\sqrt{2}$,∠A=$\frac{π}{4}$,
∴由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$可得:sinB=$\frac{bsinA}{a}$=$\frac{\sqrt{2}×\frac{\sqrt{2}}{2}}{2}$=$\frac{1}{2}$,
又∵a>b,B为锐角,
∴B=$\frac{π}{6}$,即B=30°.
故选:A.
点评 本题主要考查了正弦定理,大边对大角,特殊角的三角函数值在解三角形中的应用,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
20.函数y=x+$\frac{1}{x-1}$+1(x>1)的最小值是( )
| A. | -2 | B. | 2 | C. | -4 | D. | 4 |
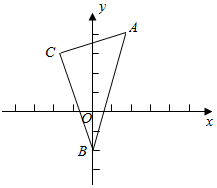 如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3),求:
如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3),求: