题目内容
14.已知直线y=kx-1和双曲线x2-y2=1的右支交于不同两点,则k的取值范围是( )| A. | $({1,\sqrt{2}})$ | B. | $({-\sqrt{2},-1})∪({1,\sqrt{2}})$ | C. | $({-\sqrt{2},\sqrt{2}})$ | D. | $({-\sqrt{2},-1})∪({-1,1})∪({1,\sqrt{2}})$ |
分析 联立直线y=kx-1和双曲线x2-y2=1,化为(1-k2)x2+2kx-2=0,由于直线y=kx-1与双曲线x2-y2=1的右支交于不同两点A,B,可得1-k2≠0.由△=4k2+8(1-k2)>0,1<k,解得即可.
解答 解:联立直线y=kx-1和双曲线x2-y2=1,化为(1-k2)x2+2kx-2=0,
∵直线y=kx-1与双曲线x2-y2=1的右支交于不同两点A,B,
∴1-k2≠0.由△=4k2+8(1-k2)>0,1<k,解得1<k<$\sqrt{2}$.
∴k的取值范围是(1,$\sqrt{2}$).
故选:A.
点评 本题综合考查了直线与双曲线的相交转化为方程联立得到△>0,属于中档题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
3.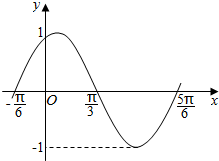 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上的所有的点( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上的所有的点( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上的所有的点( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上的所有的点( )| A. | 向左平移$\frac{π}{6}$个长度单位,再把所得各点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变 | |
| B. | 向左平移$\frac{π}{3}$个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变 | |
| C. | 向左平移$\frac{π}{3}$个长度单位,再把所得各点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变 | |
| D. | 向左平移$\frac{π}{6}$个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变 |
4.函数f(x)=x+$\frac{1}{x}$(x>0)的最小值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 与
与 平行
平行 与
与 是异面直线
是异面直线 与
与 是异面直线
是异面直线
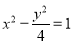 的右焦点为
的右焦点为 ,过点
,过点 ,
,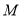 在直线
在直线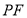 上, 且满足
上, 且满足 ,则
,则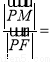 .
.