题目内容
19.若过点 M(1,0)作直线交抛物线C:y2=x于 A,B两点,且满足$\overrightarrow{{A}{M}}=λ\overrightarrow{{M}{B}}$,过 A,B两点分别作抛物线C的切线l1,l2,l1,l2的交点为 N.参考公式:过抛物线y2=2px上任一点(x0,y0)作抛物线的切线,则切线方程为yy0=p(x+x0).
(I)求证:点 N在一条定直线上;
(II)若λ∈[4,9],求直线 MN在y轴上截距的取值范围.
分析 (Ⅰ)先表示出过点A的切线和过点B的切线,然后两直线联立可求出点N的坐标,即可得到点N在定直线x=-1上;
(Ⅱ)根据$\overrightarrow{{A}{M}}=λ\overrightarrow{{M}{B}}$,可知(1-x1,-y1)=λ(x2-1,y2),进而可联立方程可求得$\frac{1}{{k}^{2}}$的表达式,进而求得范围,最后根据直线MN在y轴的截距,进而可得答案.
解答 解:(I)证明:设直线AB的方程为y=k(x-1),
联立抛物线的方程,可得ky2-y-k=0,
设A(x1,y1),B(x2,y2),可得y1y2=-1,y1+y2=$\frac{1}{k}$,
由点A处的切线的方程为y1y=$\frac{1}{2}$(x+x1),
由点B处的切线的方程为y2y=$\frac{1}{2}$(x+x2),
且y12=x1,y22=x2,
可得y1,y2是关于t的方程t2-2ty+x=0,
即有y1y2=x,
即有x=-1,即为交点N的横坐标,
故点N在一条定直线x=-1上;
(Ⅱ)∵$\overrightarrow{AM}$=λ$\overrightarrow{MB}$,∴(1-x1,-y1)=λ(x2-1,y2),
联立可得$\left\{\begin{array}{l}{-{y}_{1}=λ{y}_{2}}\\{{y}_{1}+{y}_{2}=\frac{1}{k}}\\{{y}_{1}{y}_{2}=-1}\end{array}\right.$,
$\frac{1}{{k}^{2}}$=$\frac{(1-λ)^{2}}{λ}$=$\frac{{λ}^{2}-2λ+1}{λ}$=λ+$\frac{1}{λ}$-2,4≤λ≤9,
∴$\frac{9}{4}$≤$\frac{1}{{k}^{2}}$≤$\frac{64}{9}$即有$\frac{3}{2}$≤$\frac{1}{k}$≤$\frac{8}{3}$或-$\frac{8}{3}$≤$\frac{1}{k}$≤-$\frac{3}{2}$,
由(Ⅰ)可得N(-1,$\frac{{y}_{1}+{y}_{2}}{2}$)即为(-1,$\frac{1}{2k}$),
直线MN:y=-$\frac{1}{4k}$(x-1)在y轴的截距为$\frac{1}{4k}$,
∴直线MN在x轴上截距的取值范围是[$\frac{3}{8}$,$\frac{2}{3}$]∪[-$\frac{2}{3}$,-$\frac{3}{8}$].
点评 本题主要考查了抛物线的应用,涉及了抛物线的性质,向量的计算,不等式等知识,属于中档题.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案| A. | $({1,\sqrt{2}})$ | B. | $({-\sqrt{2},-1})∪({1,\sqrt{2}})$ | C. | $({-\sqrt{2},\sqrt{2}})$ | D. | $({-\sqrt{2},-1})∪({-1,1})∪({1,\sqrt{2}})$ |
| A. | 3x-4y+2=0 | B. | 3x+4y-7=0 | C. | 3x-4y+7=0 | D. | 3x-4y-2=0 |
 ,下列结论中不正确的是( )
,下列结论中不正确的是( )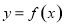 的图象关于点
的图象关于点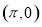 中心对称
中心对称 对称
对称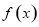 的最大值为
的最大值为