题目内容
(本小题满分12分)设直线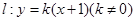 与椭圆
与椭圆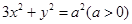 相交于
相交于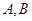 两个不同的点,与
两个不同的点,与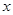 轴相交于点
轴相交于点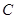 ,记
,记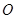 为坐标原点.
为坐标原点.
(1)证明: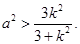
(2)若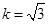 且
且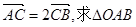 的面积及椭圆方程.
的面积及椭圆方程.
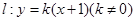 与椭圆
与椭圆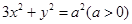 相交于
相交于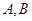 两个不同的点,与
两个不同的点,与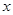 轴相交于点
轴相交于点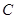 ,记
,记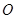 为坐标原点.
为坐标原点.(1)证明:
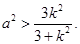
(2)若
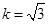 且
且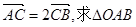 的面积及椭圆方程.
的面积及椭圆方程.(1)根据直线与椭圆联立,结合判别式大于零来得到关系式。
(2)
(2)

试题分析:(1)证明:由
 得
得 将
将 代入
代入 消去
消去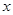 得
得 ① ………………………… 2分
① ………………………… 2分由直线l与椭圆相交于两个不同的点得
 整理得
整理得 ,即
,即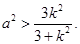 ……4分
……4分(2)解:设
 ①为
①为
得

∵
 而点
而点 , ∴
, ∴
得
 代入上式,得
代入上式,得 ……………7分
……………7分于是,△OAB的面积

 --------10分
--------10分将
 代入
代入 ,可解出
,可解出
∴△OAB的面积为
 椭圆方程是
椭圆方程是 ……………12分
……………12分点评:解决该试题的关键是通过联立方程组,得到二次方程中判别式大于零,得到证明。同时要结合向量的坐标关系,以及根与系数的关系,解得坐标,求解面积和椭圆方程。属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
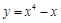 上点
上点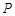 处的切线平行于直线
处的切线平行于直线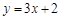 ,那么点
,那么点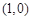
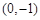
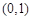
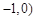
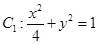 ,椭圆
,椭圆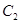 以
以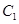 的长轴为短轴,且与
的长轴为短轴,且与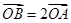 ,求直线
,求直线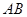 的方程.
的方程.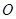 ,焦点在
,焦点在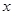 轴上,两条渐近线分别为
轴上,两条渐近线分别为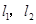 ,经过右焦点
,经过右焦点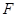 垂直于
垂直于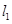 的直线分别交
的直线分别交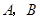 两点.已知
两点.已知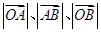 成等差数列,且
成等差数列,且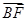 与
与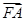 同向.
同向.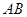 被双曲线所截得的线段的长为4,求双曲线的方程.
被双曲线所截得的线段的长为4,求双曲线的方程.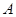 为椭圆
为椭圆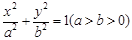 上的一个动点,弦
上的一个动点,弦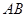 、
、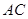 分别过焦点
分别过焦点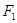 、
、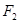 ,当
,当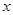 轴时,恰好有
轴时,恰好有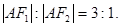
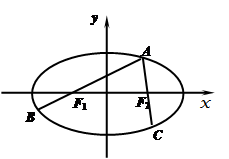
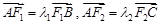 .
.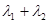 的值;
的值;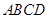 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛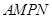 ,要求
,要求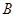 点在
点在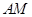 上,
上, 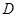 点在
点在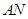 上,且对角线
上,且对角线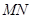 过点
过点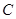 ,已知
,已知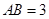 米,
米,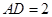 米.
米.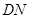 的长应在什么范围内?
的长应在什么范围内?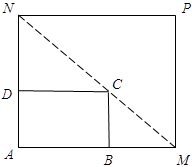
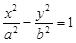 的焦距为10,点
的焦距为10,点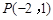 在其渐近线上,则双曲线的方程为
在其渐近线上,则双曲线的方程为
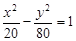

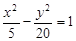
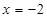 ,则抛物线方程是( )
,则抛物线方程是( )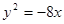 ,
,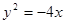
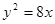
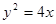
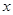 在轴上,离心率
在轴上,离心率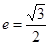 ,已知点
,已知点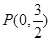 到这个椭圆上的最远距离是
到这个椭圆上的最远距离是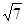 ,求这个椭圆的方程.
,求这个椭圆的方程.