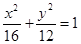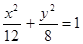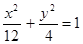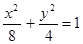题目内容
(本题满分12分)
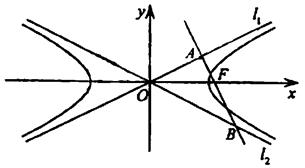
双曲线的中心为原点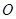 ,焦点在
,焦点在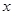 轴上,两条渐近线分别为
轴上,两条渐近线分别为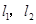 ,经过右焦点
,经过右焦点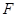 垂直于
垂直于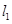 的直线分别交
的直线分别交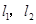 于
于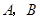 两点.已知
两点.已知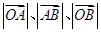 成等差数列,且
成等差数列,且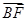 与
与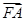 同向.
同向.
(Ⅰ)求双曲线的离心率;
(Ⅱ)设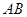 被双曲线所截得的线段的长为4,求双曲线的方程.
被双曲线所截得的线段的长为4,求双曲线的方程.
双曲线的中心为原点
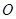 ,焦点在
,焦点在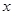 轴上,两条渐近线分别为
轴上,两条渐近线分别为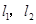 ,经过右焦点
,经过右焦点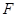 垂直于
垂直于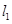 的直线分别交
的直线分别交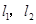 于
于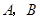 两点.已知
两点.已知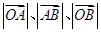 成等差数列,且
成等差数列,且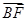 与
与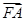 同向.
同向.(Ⅰ)求双曲线的离心率;
(Ⅱ)设
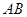 被双曲线所截得的线段的长为4,求双曲线的方程.
被双曲线所截得的线段的长为4,求双曲线的方程.(Ⅰ)e= =
=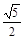 ;(Ⅱ)
;(Ⅱ)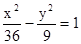 。
。
 =
=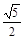 ;(Ⅱ)
;(Ⅱ)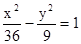 。
。试题分析:(Ⅰ)设
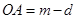 ,
,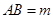 ,
,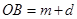
由勾股定理可得:

得:
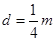 ,
,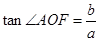 ,
,
由倍角公式
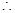
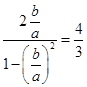 ,解得
,解得 ,则离心率
,则离心率 .
.(Ⅱ)过
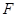 直线方程为
直线方程为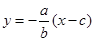 ,与双曲线方程
,与双曲线方程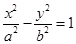 联立
联立将
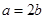 ,
,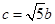 代入,
代入,化简有


将数值代入,有
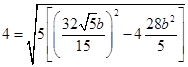 ,解得
,解得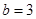
故所求的双曲线方程为
 .
.解法二:解:(Ⅰ)设双曲线方程为
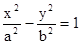 (a>0,b>0),右焦点为F(c,0)(c>0),则c2=a2+b2
(a>0,b>0),右焦点为F(c,0)(c>0),则c2=a2+b2不妨设l1:bx-ay=0,l2:bx+ay=0
则
 ,
,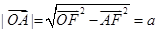
因为
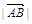 2+
2+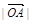 2=
2=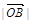 2,且
2,且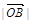 =2
=2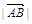 -
-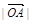 ,
,所以
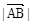 2+
2+ 2=(2
2=(2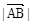 -
- )2,
)2,于是得tan∠AOB=
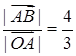 。
。又
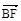 与
与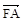 同向,故∠AOF=
同向,故∠AOF= ∠AOB,
∠AOB,所以
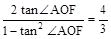
解得 tan∠AOF=
 ,或tan∠AOF=-2(舍去)。
,或tan∠AOF=-2(舍去)。因此

所以双曲线的离心率e=
 =
=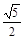
(Ⅱ)由a=2b知,双曲线的方程可化为
x2-4y2=4b2 ①
由l1的斜率为
 ,c=
,c=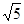 b知,直线AB的方程为
b知,直线AB的方程为y=-2(x-
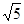 b) ②
b) ②将②代入①并化简,得
15x2-32
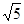 bx+84b2=0
bx+84b2=0设AB与双曲线的两交点的坐标分别为(x1,y1),(x2,y2),则
x1+x2=
 ,x1·x2=
,x1·x2=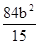 ③
③AB被双曲线所截得的线段长
l=
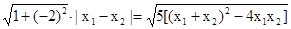 ④
④将③代入④,并化简得l=
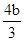 ,而由已知l=4,故b=3,a=6
,而由已知l=4,故b=3,a=6所以双曲线的方程为
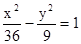
点评:中档题,涉及直线与圆锥曲线的位置关系问题,往往要利用韦达定理。弦长问题,往往利用弦长公式,通过整体代换,简化解题过程。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
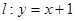 与曲线
与曲线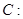
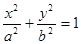
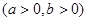 交于不同的两点
交于不同的两点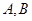 ,
,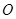 为坐标原点.
为坐标原点.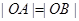 ,求证:曲线
,求证:曲线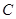 是一个圆;
是一个圆; ,当
,当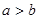 且
且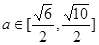 时,求曲线
时,求曲线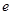 的取值范围.
的取值范围.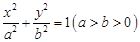 的离心率
的离心率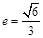 ,过点
,过点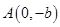 和
和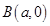 的直线与原点的距离为
的直线与原点的距离为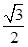 。⑴求椭圆的方程;⑵已知定点
。⑴求椭圆的方程;⑵已知定点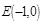 ,若直线
,若直线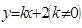 与椭圆交于
与椭圆交于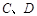 两点,问:是否存在
两点,问:是否存在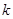 的值,使以
的值,使以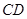 为直径的圆过
为直径的圆过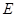 点?请说明理由。
点?请说明理由。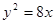 的焦点为
的焦点为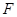 ,准线为
,准线为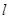 ,
,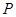 为抛物线上的一点,
为抛物线上的一点,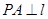 ,垂足为
,垂足为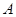 .若直线
.若直线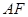 的斜率为
的斜率为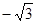 ,则
,则
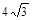
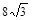
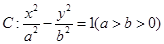 的右焦点为
的右焦点为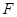 ,左右顶点分别为
,左右顶点分别为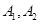 ,过
,过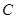 的一条渐近线平行的直线
的一条渐近线平行的直线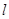 与另一条渐近线相交于
与另一条渐近线相交于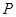 ,若
,若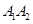 为直径的圆上,则双曲线的离心率为________ ______.
为直径的圆上,则双曲线的离心率为________ ______.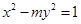 的实轴长是虚轴长的2倍,则rn=
的实轴长是虚轴长的2倍,则rn=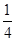
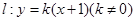 与椭圆
与椭圆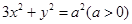 相交于
相交于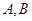 两个不同的点,与
两个不同的点,与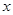 轴相交于点
轴相交于点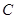 ,记
,记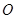 为坐标原点.
为坐标原点.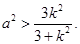
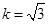 且
且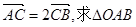 的面积及椭圆方程.
的面积及椭圆方程.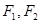 是椭圆
是椭圆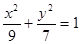 的两个焦点,
的两个焦点,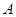 为椭圆上的一点,且
为椭圆上的一点,且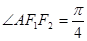 ,则
,则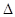
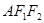 的面积是( )
的面积是( )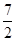
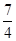
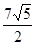
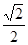 ,则该椭圆的方程为
,则该椭圆的方程为