题目内容
1.点(0,0)和点(-1,1)在直线2x+y+m=0的同侧,则m的取值范围是( )| A. | m>1或m<0 | B. | m>2或m<1 | C. | 0<m<1 | D. | 1<m<2 |
分析 由点(-1,1)和原点位于直线2x+y+m=0的同侧可得,m(-2+1+m)>0,解不等式可求m得范围.
解答 解:由题意可得,m(-2+1+m)>0,
m(m-1)>0
m<0或m>1
故选:A.
点评 本题主要考查了二元一次不等式表示平面区域,在直线同一侧的点的坐标代入ax+by+c中的函数值的符号相同,两侧的点的坐标代入ax+by+c中的函数值的符号相反.

练习册系列答案
相关题目
9.下列函数中x=0是极值点的函数是( )
| A. | f(x)=-x3 | B. | f(x)=x2 | C. | f(x)=sinx-x | D. | f(x)=$\frac{1}{x}$ |
16.已知集合A={y|y=x${\;}^{\frac{2}{3}}$,x≥1},B={y|y=($\frac{1}{2}$)x,x≥-1},则A∩B=( )
| A. | {y|1≤y≤2} | B. | {y|y≥2} | C. | {y|$\frac{1}{2}$≤y≤1} | D. | {y|y≥1} |
11.有一段演绎推理是这样的:“因为一次函数y=kx+b(k≠0)在R上是增函数,而y=-x+2是一次函数,所以y=-x+2在R上是增函数”的结论显然是错误,这是因为( )
| A. | 大前提错误 | B. | 小前提错误 | C. | 推理形式错误 | D. | 非以上错误 |
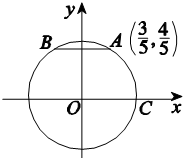 如图所示,A,B是单位圆O上的点,且B在第二象限,C是圆与x轴正半轴的交点,A点的坐标为($\frac{3}{5}$,$\frac{4}{5}$),且A与B关于y轴对称.
如图所示,A,B是单位圆O上的点,且B在第二象限,C是圆与x轴正半轴的交点,A点的坐标为($\frac{3}{5}$,$\frac{4}{5}$),且A与B关于y轴对称.