题目内容
7.已知向量$\overrightarrow a$=(4,-2),$\overrightarrow b$=(-1,3),$\overrightarrow c$=(6,8).(1)求($\overrightarrow a$+$\overrightarrow b$)•$\overrightarrow c$;
(2)若$\overrightarrow a$⊥($\overrightarrow b$-λ$\overrightarrow c$),求实数λ的值.
分析 (1)容易求出向量$\overrightarrow{a}+\overrightarrow{b}$的坐标,然后进行向量数量积的坐标运算即可求出$(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{c}$的值;
(2)根据条件可以求出$\overrightarrow{a}•\overrightarrow{b}=-10,\overrightarrow{a}•\overrightarrow{c}=8$,而由$\overrightarrow{a}⊥(\overrightarrow{b}-λ\overrightarrow{c})$可得到$\overrightarrow{a}•(\overrightarrow{b}-λ\overrightarrow{c})=0$,从而得到关于λ的方程,解出λ即可.
解答 解:(1)$\overrightarrow{a}+\overrightarrow{b}=(3,1)$,$\overrightarrow{c}=(6,8)$;
∴$(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{c}=18+8=26$;
(2)$\overrightarrow{a}•\overrightarrow{b}=-4-6=-10,\overrightarrow{a}•\overrightarrow{c}=24-16=8$;
∵$\overrightarrow{a}⊥(\overrightarrow{b}-λ\overrightarrow{c})$;
∴$\overrightarrow{a}•(\overrightarrow{b}-λ\overrightarrow{c})=\overrightarrow{a}•\overrightarrow{b}-λ\overrightarrow{a}•\overrightarrow{c}$
=-10-8λ
=0;
∴$λ=-\frac{5}{4}$.
点评 考查向量坐标的加法运算,向量坐标的数量积运算,以及向量垂直的充要条件,向量数量积的运算.

| 场数 | 9 | 10 | 11 | 12 | 13 | 14 |
| 人数 | 10 | 18 | 22 | 25 | 20 | 5 |
根据已知条件完成下面的2×2列联表,并据此资料判断我们能否有95%的把握认为“歌迷”与性别有关?
| 非歌迷 | 歌迷 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
| P(K2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | f(-π)>f(log2$\frac{1}{4}$)>f($-\frac{π}{2}$) | B. | f(log2$\frac{1}{4}$)>f(-$\frac{π}{2}$)>f(-π) | ||
| C. | f(-π)>f(-$\frac{π}{2}$)>f(log2$\frac{1}{4}$) | D. | f(-$\frac{π}{2}$)>f(log2$\frac{1}{4}$)>f(-π) |
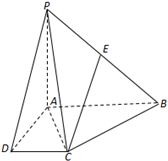 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=AD=2DC=2$\sqrt{2}$,PA=4且E为PB的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=AD=2DC=2$\sqrt{2}$,PA=4且E为PB的中点.