题目内容
14.已知函数f(x)的图象与函数y=x3-3x2+2的图象关于点($\frac{1}{2}$,0)对称,过点(1,t)仅能作曲线y=f(x)的一条切线,则实数t的取值范围是( )| A. | (-3,-2) | B. | [-3,-2] | C. | (-∞,-3)∪(-2,+∞) | D. | (-∞,-3)∪[-2,+∞) |
分析 由对称性可得(x,y)为y=f(x)图象上的点,其对称点为(1-x,-y),且在函数y=x3-3x2+2的图象上,代入可得f(x)的解析式,设出切点(m,n),求出f(x)的导数,可得切线的斜率和方程,代入点(1,t),化简整理可得t+3=3m2-2m3,
由g(m)=3m2-2m3,求出导数和单调区间、极值,由题意可得t+3=3m2-2m3只有一解,则t+3>1或t+3<0,解不等式即可得到所求范围.
解答 解:函数f(x)的图象与函数y=x3-3x2+2的图象关于点($\frac{1}{2}$,0)对称,
设(x,y)为y=f(x)图象上的点,其对称点为(1-x,-y),且在函数y=x3-3x2+2的图象上,
可得-y=(1-x)3-3(1-x)2+2,即为y=f(x)=(x-1)3+3(1-x)2-2,
设切点为(m,n),则n=(m-1)3+3(1-m)2-2,
f(x)的导数为f′(x)=3(x-1)2+6(x-1)=3(x2-1),
可得切线的方程为y-n=3(m2-1)(x-m),
代入点(1,t),可得t-n=3(m2-1)(1-m),
化简可得t+3=3m2-2m3,
由g(m)=3m2-2m3,
g′(m)=6m-6m2=6m(1-m),
当0<m<1时,g′(m)>0,g(m)递增;当m<0或m>1时,g′(m)<0,g(m)递减.
则g(m)在m=0处取得极小值0,在m=1处取得极大值1,
由过点(1,t)仅能作曲线y=f(x)的一条切线,
可得t+3=3m2-2m3只有一解,
则t+3>1或t+3<0,
解得t>-2或t<-3.
故选:C.
点评 本题主要考查导数的运用:求切线的方程和单调区间、极值,考查转化思想的运用,以及化简整理能力,属于中档题.

练习册系列答案
相关题目
5.i为虚数单位,已知复数z满足$\frac{2}{1+i}=\overline z+i$,则z=( )
| A. | 1+2i | B. | 1-2i | C. | 1+i | D. | -1+i |
9. 我国古代数学家祖暅是著名数学家祖冲之之子,祖暅原理叙述道:“夫叠棋成立积,缘幂势既同,则积不容异.”意思是:夹在两个平行平面之间的两个几何体被平行于这两个平行平面的任意平面所截,如果截得的两个截面面积总相等,那么这两个几何体的体积相等.其最著名之处是解决了“牟合方盖”中的体积问题,其核心过程为:如下图正方体ABCD-A1B1C1D1,求图中四分之一圆柱体BB1C1-AA1D1和四分之一圆柱体AA1B1-DD1C1公共部分的体积V,若图中正方体的棱长为2,则V=( )
我国古代数学家祖暅是著名数学家祖冲之之子,祖暅原理叙述道:“夫叠棋成立积,缘幂势既同,则积不容异.”意思是:夹在两个平行平面之间的两个几何体被平行于这两个平行平面的任意平面所截,如果截得的两个截面面积总相等,那么这两个几何体的体积相等.其最著名之处是解决了“牟合方盖”中的体积问题,其核心过程为:如下图正方体ABCD-A1B1C1D1,求图中四分之一圆柱体BB1C1-AA1D1和四分之一圆柱体AA1B1-DD1C1公共部分的体积V,若图中正方体的棱长为2,则V=( )
(在高度h处的截面:用平行于正方体上下底面的平面去截,记截得两圆柱体公共部分所得面积为S1,截得正方体所得面积为S2,截得锥体所得面积为S3,${S_1}={R^2}-{h^2}$,${S_2}={R^2}$⇒S2-S1=S3)
 我国古代数学家祖暅是著名数学家祖冲之之子,祖暅原理叙述道:“夫叠棋成立积,缘幂势既同,则积不容异.”意思是:夹在两个平行平面之间的两个几何体被平行于这两个平行平面的任意平面所截,如果截得的两个截面面积总相等,那么这两个几何体的体积相等.其最著名之处是解决了“牟合方盖”中的体积问题,其核心过程为:如下图正方体ABCD-A1B1C1D1,求图中四分之一圆柱体BB1C1-AA1D1和四分之一圆柱体AA1B1-DD1C1公共部分的体积V,若图中正方体的棱长为2,则V=( )
我国古代数学家祖暅是著名数学家祖冲之之子,祖暅原理叙述道:“夫叠棋成立积,缘幂势既同,则积不容异.”意思是:夹在两个平行平面之间的两个几何体被平行于这两个平行平面的任意平面所截,如果截得的两个截面面积总相等,那么这两个几何体的体积相等.其最著名之处是解决了“牟合方盖”中的体积问题,其核心过程为:如下图正方体ABCD-A1B1C1D1,求图中四分之一圆柱体BB1C1-AA1D1和四分之一圆柱体AA1B1-DD1C1公共部分的体积V,若图中正方体的棱长为2,则V=( ) (在高度h处的截面:用平行于正方体上下底面的平面去截,记截得两圆柱体公共部分所得面积为S1,截得正方体所得面积为S2,截得锥体所得面积为S3,${S_1}={R^2}-{h^2}$,${S_2}={R^2}$⇒S2-S1=S3)
| A. | $\frac{16}{3}$ | B. | $\frac{8}{3}$ | C. | 8 | D. | $\frac{8π}{3}$ |
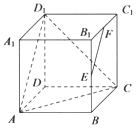 如图,在正方体ABCD-A1B1C1D1中,点E,F分别为BB1,B1C1的中点.
如图,在正方体ABCD-A1B1C1D1中,点E,F分别为BB1,B1C1的中点.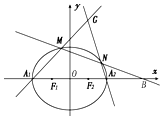 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A1,A2,左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,点B(4,0),F2为线段A1B的中点.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A1,A2,左、右焦点分别为F1,F2,离心率为$\frac{1}{2}$,点B(4,0),F2为线段A1B的中点.