题目内容
(本小题满分12分)
已知:如图,在四棱锥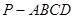 中,四边形
中,四边形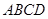 为正方形,
为正方形,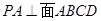 ,且
,且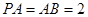 ,
,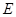 为
为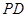 中点.
中点.
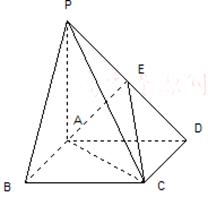
(1)证明: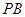 //平面
//平面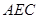 ;
;
(2)证明:平面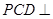 平面
平面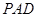 ;
;
(3)求二面角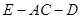 的正弦值.
的正弦值.
已知:如图,在四棱锥
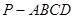 中,四边形
中,四边形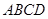 为正方形,
为正方形,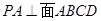 ,且
,且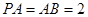 ,
,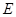 为
为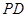 中点.
中点.
(1)证明:
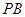 //平面
//平面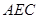 ;
;(2)证明:平面
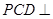 平面
平面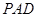 ;
;(3)求二面角
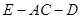 的正弦值.
的正弦值.(1) 结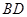 交
交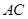 于点
于点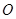 ,连结
,连结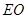 ,那么根据中位线性质可知
,那么根据中位线性质可知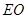 //
//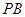 ,那么结合线面平行的判定定理来得到。
,那么结合线面平行的判定定理来得到。
(2)建立空间直角坐标系,然后结合空间向量的平面的法向量,借助于法向量的垂直来证明面面垂直。
(3)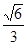
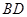 交
交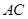 于点
于点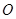 ,连结
,连结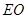 ,那么根据中位线性质可知
,那么根据中位线性质可知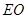 //
//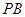 ,那么结合线面平行的判定定理来得到。
,那么结合线面平行的判定定理来得到。(2)建立空间直角坐标系,然后结合空间向量的平面的法向量,借助于法向量的垂直来证明面面垂直。
(3)
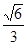
试题分析:解:(1)
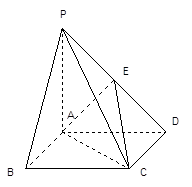
证明:连结
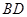 交
交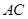 于点
于点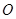 ,连结
,连结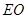 ……………………1分
……………………1分
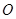 为
为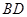 中点,
中点,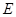 为
为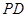 中点,
中点,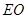 //
//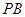 ……………………2分
……………………2分
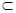 平面
平面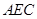 ,
,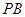
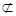 平面
平面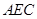 , ………3分
, ………3分∴
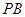 //平面
//平面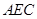 .
. (2)证明:
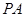 ⊥平面
⊥平面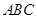
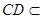 平面
平面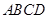 ,
,
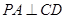 . …………4分
. …………4分又
 在正方形
在正方形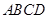 中
中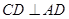 且
且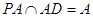 , …5分
, …5分∴
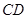
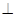 平面
平面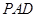 . ……………………6分
. ……………………6分又
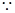
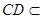 平面
平面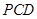 ,
,∴平面
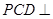 平面
平面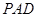 . ……………………7分
. ……………………7分(3)如图,以
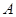 为坐标原点,
为坐标原点,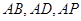 所在直线分别为
所在直线分别为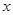 轴,
轴,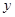 轴,
轴,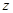 轴建立空
轴建立空间直角坐标系.
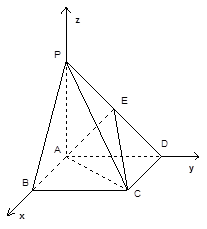
由
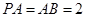 可知
可知 的坐标分别为
的坐标分别为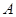 (0, 0, 0),
(0, 0, 0), 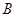 (2, 0, 0),
(2, 0, 0),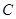 (2, 2, 0),
(2, 2, 0), 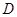 (0, 2, 0),
(0, 2, 0), 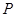 (0, 0, 2),
(0, 0, 2), 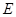 (0, 1, 1) .………9分
(0, 1, 1) .………9分
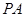
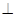 平面
平面 ,∴
,∴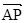 是平面
是平面 的法向量,
的法向量,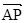 =(0, 0, 2).
=(0, 0, 2).设平面
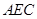 的法向量为
的法向量为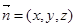 ,
, 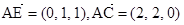 ,
, 则
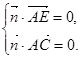 即
即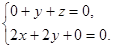
∴
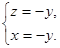
∴ 令
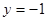 ,则
,则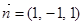 . ………………11分
. ………………11分∴
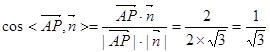 ,
, 二面角
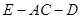 的正弦值为
的正弦值为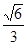 …………………12分
…………………12分点评:解决证明试题,一般要运用线面平行的判定定理以及面面垂直的判定定理,来分析得到,而对于求解二面角一般可以运用定义法,或者是三垂线定理法,以及向量法来表示得到,属于中档题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
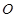 的面上有四点
的面上有四点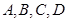 ,
,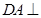 平面
平面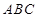 ,
,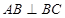 ,
, ,则球
,则球
 ABC=60
ABC=60 ,EC
,EC 面ABCD,FA
面ABCD,FA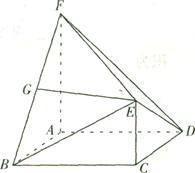
 中,下列结论错误的是
中,下列结论错误的是 ∥平面
∥平面
 平面
平面

 与
与 所成的角是45º
所成的角是45º 中,
中, 底面
底面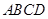 ,
,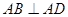 ,
,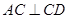 ,
,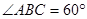 ,
,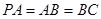 ,
,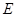 是
是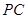 的中点。
的中点。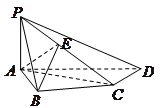
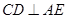 ;
;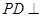 平面
平面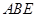 ;
;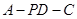 的正切值.
的正切值.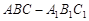 中,
中,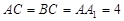 ,
, 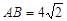 ,若
,若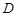 是
是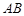 中点.
中点.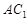 ∥平面
∥平面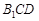 ;
; 所成的角.
所成的角.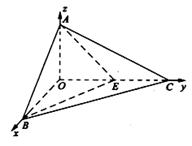
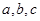 ,若
,若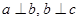 ,则
,则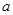 ∥
∥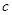 ;②
;②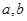 是异面直线,
是异面直线,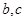 是异面直线,则
是异面直线,则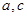 不一定是异面直线;③过空间任一点,有且仅有一条直线和已知平面
不一定是异面直线;③过空间任一点,有且仅有一条直线和已知平面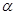 垂直;④平面
垂直;④平面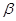 ,点
,点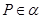 ,直线
,直线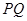 //
//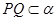 ;其中正确的命题的个数有( )
;其中正确的命题的个数有( )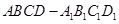 中,
中,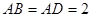 ,
,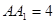 ,点
,点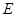 在
在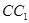 上,且
上,且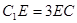 .
.
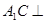 平面
平面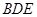 ;
;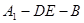 的余弦值.
的余弦值.