Question

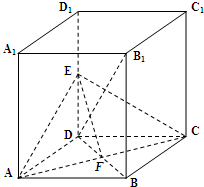
如图，在正四棱柱ABCD-A₁B₁C₁D₁中，AA1=

2

，AB=1，E是DD₁的中点．
（1）求证：AC⊥B₁D；
（2）求二面角E-AC-B的大小．

Answer 1

（本小题满分14分）
解法一：
（1）证明：连接BD．
∵ABCD-A₁B₁C₁D₁是正四棱柱，∴B₁B⊥平面ABCD，
∴BD是B₁D在平面ABCD上的射影，…．（2分）
∵底面ABCD是正方形，∴AC⊥BD，…．（4分）
根据三垂线定理∴AC⊥B₁D．…..（6分）
（2）设AC∩BD=F，连接EF．∵DE⊥平面ABCD，且AC⊥BD，…（7分）
根据三垂线定理得AC⊥FE，又AC⊥FB，∴∠EFB是二面角E-AC-B的平面角．…..（9分）
在Rt△EDF中，由DE=DF=

2

2

，得∠EFD=45°．…..（12分）
∴∠EFB=180°-45°=135°，…（13分）
即二面角E-AC-B的大小是135°．…..（14分）

解法二：∵ABCD-A₁B₁C₁D₁是正四棱柱，∴DA、DC、DD₁两两互相垂直
如图，以D为原点，直线DA，DC，DD₁分别为x轴，y轴，z轴，建立空间直角坐标系．…．（1分）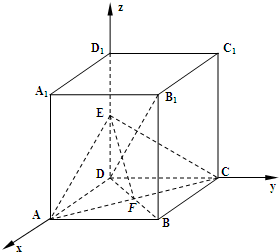

D(0，0，0)，A(1，0，0)，B(1，1，0)， C(0，1，0)，B1(1，1， 2 )

…..（3分）
（1）证明：
∵

AC

=(-1，1，0)，

DB1

=(1，1，

2

)…．（4分）
∴

AC

•

DB1

=0，∴AC⊥B₁D．…..（6分）

（2）
连接BD，设AC∩BD=F，连接EF．
∵DE⊥平面ABCD，且AC⊥BD∴AC⊥FE，AC⊥FB…（8分）
∴∠EFB是二面角E-AC-B的平面角．…..（9分）
∵底面ABCD是正方形
∴F(

1

2

，

1

2

，0)，∴

FB

=(

1

2

，

1

2

，0)，

FE

=(-

1

2

，-

1

2

，

2

2

)，．…．（11分）
…..（13分）
∴cos＜

FB

，

FE

＞=

FB • FE

| FB || FE |

=-

2

2

…（13分）

∴二面角E-AC-B的大小是135°．…..（14分）