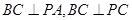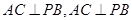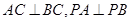题目内容
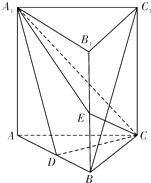
如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=
AB.
(Ⅰ)证明:BC1∥平面A1CD
(Ⅱ)求二面角D-A1C-E的正弦值.
| ||
| 2 |
(Ⅰ)证明:BC1∥平面A1CD
(Ⅱ)求二面角D-A1C-E的正弦值.

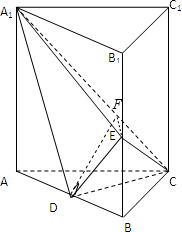
(Ⅰ)证明:连结AC1交A1C于点F,则F为AC1的中点,
又D是AB中点,连结DF,则BC1∥DF,
因为DF?平面A1CD,BC1?平面A1CD,
所以BC1∥平面A1CD.
(Ⅱ)因为直棱柱ABC-A1B1C1,所以AA1⊥CD,
由已知AC=CB,D为AB的中点,所以CD⊥AB,
又AA1∩AB=A,于是,CD⊥平面ABB1A1,
设AB=2
,则AA1=AC=CB=2,得∠ACB=90°,
CD=
,A1D=
,DE=
,A1E=3
故A1D2+DE2=A1E2,即DE⊥A1D,所以DE⊥平面A1DC,
又A1C=2
,过D作DF⊥A1C于F,∠DFE为二面角D-A1C-E的平面角,
在△A1DC中,DF=
=
,EF=
=
,
所以二面角D-A1C-E的正弦值.sin∠DFE=
=
.
又D是AB中点,连结DF,则BC1∥DF,
因为DF?平面A1CD,BC1?平面A1CD,
所以BC1∥平面A1CD.
(Ⅱ)因为直棱柱ABC-A1B1C1,所以AA1⊥CD,
由已知AC=CB,D为AB的中点,所以CD⊥AB,
又AA1∩AB=A,于是,CD⊥平面ABB1A1,
设AB=2
| 2 |
CD=
| 2 |
| 6 |
| 3 |
故A1D2+DE2=A1E2,即DE⊥A1D,所以DE⊥平面A1DC,
又A1C=2
| 2 |
在△A1DC中,DF=
| A1D•DC |
| A1C |
| ||
| 2 |
| DE2+DF2 |
3
| ||
| 2 |
所以二面角D-A1C-E的正弦值.sin∠DFE=
| DE |
| EF |
| ||
| 3 |


练习册系列答案
相关题目
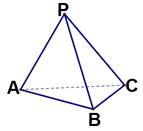
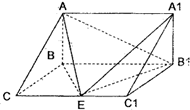
 的底面是直角三角形,
的底面是直角三角形, ,点
,点 在底面内的射影恰好是
在底面内的射影恰好是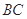 的中点,且
的中点,且


 平面
平面 ;
; ,求点
,求点 到平面
到平面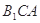 的距离.
的距离.

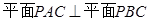 的条件是( )
的条件是( )