题目内容

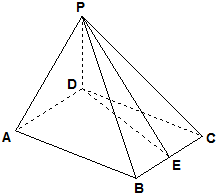
如图，正方形ABCD所在平面与矩形ACEF所在平面垂直，其中AB=
2
，AF=1，M是EF中点．
（1）求证：AM∥平面BDE；
（2）求二面角A-BD-F的大小．
（1）证：∵M为中点
∴EM
∥
.
.
OA，故EMAO为平行四边形，AM∥OE
∴AM∥平面BDE（6分）
（2）∵FA⊥AC，平面FACE⊥平面ABCD
∴FA⊥平面ABCD
∵AO⊥BD∴FO⊥BD∴∠FOA为二面角A-BD-F的平面角
在Rt△FOA中，OA=1，AF=1
∴∠FOA=45°
即二面角A-BD-F的大小为45°（13分）
练习册系列答案
相关题目
已知△ABC和△DBC所在的平面互相垂直，且AB=BC=BD，∠CBA=∠DBC=120°，则AB与平面ADC所成角的正弦值为______．
如图，四棱锥P-ABCD是底面边长为1的正方形，PD⊥BC，PD=1，PC=
2
．
（Ⅰ）求证：PD⊥面ABCD；
（Ⅱ）求二面角A-PB-D的大小．
在直角梯形ABCD中，∠D=∠BAD=90°，AD=DC=
1
2
AB=1，将△ADC沿AC折起，使D到D′．若二面角D′-AC-B为60°，则三棱锥D′-ABC的体积为______．
设正方体ABC-A1B1C1D1的棱长为2，动点E，F在棱A1B1上，动点P、Q分别在棱AD、CD上，若EF=1，A1E=x，DQ=y，DP=z（x，y，z＞0），则下列结论中错误的是（　　）
A．EF∥平面DPQ
B．二面角P-EF-Q所成角的最大值为
π
4
C．三棱锥P-EFQ的体积与y的变化有关，与x、z的变化无关
D．异面直线EQ和AD1所成角的大小与x、y的变化无关
二面角α-EF-β的大小为120°，A是它内部的一点AB⊥α，AC⊥β，B，C分别为垂足．
（1）求证：平面ABC⊥β；
（2）当AB=4cm，AC=6cm，求BC的长及A到EF的距离．
如图，已知四棱锥P-ABCD的底面为菱形，∠BCD=60°，PD⊥AD．点E是BC边上的中点．
（1）求证：AD⊥面PDE；
（2）若二面角P-AD-C的大小等于60°，且AB=4，PD=
8
3
3
；①求VP-ABED；②求二面角P-AB-C大小．
如图，在正四棱柱ABCD-A1B1C1D1中，AA1=
2
，AB=1，E是DD1的中点．
（1）求证：AC⊥B1D；
（2）求二面角E-AC-B的大小．
如图，AB是圆的直径，PA垂直圆所在的平面，C是圆上的点．
（Ⅰ）求证：平面PAC⊥平面PBC；
（Ⅱ）若AB=2，AC=1，PA=1，求证：二面角C-PB-A的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网