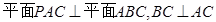题目内容
三棱柱ABC-A1B1C1中,∠ABC=90°,BB1⊥底面ABC,D为棱AC的中点,E为棱A1C1的中点,且AB=BC=BB1=1.
(1)求证:CE∥平面BA1D.
(2)求二面角A1-BD-C的余弦值.
(3)棱CC1上是否存在一点P,使PD⊥平面A1BD,若存在,试确定P点位置,若不存在,请说明理由.
(1)求证:CE∥平面BA1D.
(2)求二面角A1-BD-C的余弦值.
(3)棱CC1上是否存在一点P,使PD⊥平面A1BD,若存在,试确定P点位置,若不存在,请说明理由.

方法一:(几何法)
证明:(1)因为E、D分别是A1C1和AC的中点,则A1E∥CD且A1E=CD,
则CE∥A1D….(2分),而CE?平面BA1D,A1D?平面BA1D,则CE∥平面BA1D…(4分)
(2)因为B1B⊥平面ABC,故A1A⊥平面ABC,所以AA1⊥BD
又AB=BC=1且D为AC的中点,故BD⊥AC,
而AA1∩AC=A,BD⊥平面A1ACC1
所以A1D⊥BD,AD⊥BD
故∠A1DA为所求二面角A1-BD-C的平面角的补角.…(6分)
在Rt△A1AD中,A1D=
=
所以cos∠A1DA=
=
故所求二面角的余弦值为cos(π-∠A1DA)=-
…(8分)
(3)P为CC1中点时,即PC=
,PD⊥平面A1BD.
因为tan∠A1DA=
=
=
,所以tan∠A1DA•tan∠PDC=
•
=1
即∠A1DA+∠PDC=90°,即∠A1DP=90°,即PD⊥A1D…(10分)
由(2)知,BD⊥平面A1ACC1,PD?平面A1ACC1
所以BD⊥PD,又BD∩A1D=D.
所以PD⊥平面A1BD.…(12分)
方法二:(向量法)
证明:(1)以B为坐标原点,射线BC为x轴的正半轴,建立如图所示的直角坐标系B-xyz
则A(0,1,0),C(1,0,0),D(
,
,0),B1(0,0,1),A1(0,1,1),C1(1,0,1),E(
,
,1)
设平面A1BD的一个法向量n1=(x,y,z)
又
=(0,1,1)
=(
,
,0)
令x=1可得n1n1=(1,-1,1)…(2分)
=(-
,
,1),n1•
=0
又因为CE?平面A1BD,故CE∥平面BA1D.…(4分)
(2)又平面BDC的一个法向量为n2=(0,0,1),平面A1BD的一个法向量n1=(1,-1,1)…(6分)
设二面角A1-BD-C的大小为θ,可知θ为钝角,
故cosθ=-
=-
…(8分)
(3)设P(1,0,z)则
=(
,-
,z)…(9分)
要使PD⊥平面A1BD,则需
…(10分)
可得z=
,故P(1,0,
)
即当P是C1C的中点时,
所以PD⊥平面A1BD.…(12分)

证明:(1)因为E、D分别是A1C1和AC的中点,则A1E∥CD且A1E=CD,
则CE∥A1D….(2分),而CE?平面BA1D,A1D?平面BA1D,则CE∥平面BA1D…(4分)
(2)因为B1B⊥平面ABC,故A1A⊥平面ABC,所以AA1⊥BD
又AB=BC=1且D为AC的中点,故BD⊥AC,
而AA1∩AC=A,BD⊥平面A1ACC1
所以A1D⊥BD,AD⊥BD
故∠A1DA为所求二面角A1-BD-C的平面角的补角.…(6分)
在Rt△A1AD中,A1D=
12+(
|
| ||
| 2 |
所以cos∠A1DA=
| AD |
| A1D |
| ||
| 3 |
故所求二面角的余弦值为cos(π-∠A1DA)=-
| ||
| 3 |
(3)P为CC1中点时,即PC=
| 1 |
| 2 |
因为tan∠A1DA=
| AA1 |
| AD |
| 1 | ||||
|
| 2 |
| 2 |
| ||||
|
即∠A1DA+∠PDC=90°,即∠A1DP=90°,即PD⊥A1D…(10分)
由(2)知,BD⊥平面A1ACC1,PD?平面A1ACC1
所以BD⊥PD,又BD∩A1D=D.
所以PD⊥平面A1BD.…(12分)
方法二:(向量法)
证明:(1)以B为坐标原点,射线BC为x轴的正半轴,建立如图所示的直角坐标系B-xyz
则A(0,1,0),C(1,0,0),D(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
设平面A1BD的一个法向量n1=(x,y,z)
又
| BA1 |
| BD |
| 1 |
| 2 |
| 1 |
| 2 |
|
令x=1可得n1n1=(1,-1,1)…(2分)
| CE |
| 1 |
| 2 |
| 1 |
| 2 |
| CE |
又因为CE?平面A1BD,故CE∥平面BA1D.…(4分)
(2)又平面BDC的一个法向量为n2=(0,0,1),平面A1BD的一个法向量n1=(1,-1,1)…(6分)
设二面角A1-BD-C的大小为θ,可知θ为钝角,
故cosθ=-
| |n1n1•n2| |
| |n1n1||n2n2| |
| ||
| 3 |
(3)设P(1,0,z)则
| DP |
| 1 |
| 2 |
| 1 |
| 2 |
要使PD⊥平面A1BD,则需
|
可得z=
| 1 |
| 2 |
| 1 |
| 2 |
即当P是C1C的中点时,
所以PD⊥平面A1BD.…(12分)


练习册系列答案
相关题目




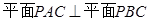 的条件是( )
的条件是( )