题目内容
4.已知数列{an}中,a1=-$\frac{5}{12}$,nan+1=(n+1)an+$\frac{n}{n+3}$,则该数列的通项an=-$\frac{n(2n+3)}{2(n+1)(n+2)}$.分析 在等式的两边同时除以n(n+1),得$\frac{{a}_{n+1}}{n+1}$-$\frac{{a}_{n}}{n}$=$\frac{1}{2}$($\frac{1}{n+1}$-$\frac{1}{n+3}$),然后利用累加法求数列的通项公式即可.
解答 解:∵nan+1=(n+1)an+$\frac{n}{n+3}$,
∴在等式的两边同时除以n(n+1),得$\frac{{a}_{n+1}}{n+1}$-$\frac{{a}_{n}}{n}$=$\frac{1}{2}$($\frac{1}{n+1}$-$\frac{1}{n+3}$),
所以$\frac{{a}_{n}}{n}$=a1+$\frac{1}{2}$[($\frac{1}{n}$-$\frac{1}{n+2}$)+($\frac{1}{n-1}$-$\frac{1}{n+1}$)+…+($\frac{1}{2}$-$\frac{1}{4}$)]=-$\frac{5}{12}$+$\frac{1}{2}$($\frac{1}{2}$+$\frac{1}{3}$-$\frac{1}{n+2}$-$\frac{1}{n+1}$),
所以an=-$\frac{n(2n+3)}{2(n+1)(n+2)}$,
故答案为:-$\frac{n(2n+3)}{2(n+1)(n+2)}$.
点评 本题主要考查利用累加法求数列的通项公式,以及利用裂项法求数列的和,要使熟练掌握这些变形技巧.

练习册系列答案
相关题目
15.已知双曲线C:${x^2}-\frac{y^2}{3}=1$的左、右焦点分别是F1,F2,若A是双曲线右支上一点且满足$∠{F_1}A{F_2}={60^o}$,则${S_{△{F_1}A{F_2}}}$=( )
| A. | $3\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | 3 |
16.双曲线$\frac{x^2}{m}-\frac{y^2}{4}=1$的焦点与椭圆$\frac{x^2}{20}+\frac{y^2}{4}=1$的焦点重合,则m的值等于( )
| A. | 12 | B. | 20 | C. | $2\sqrt{3}$ | D. | $2\sqrt{5}$ |
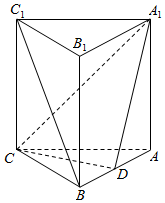 已知:三棱柱ABC-A1B1C1中,A1A⊥平面ABC,CA=CB,D是AB的中点,E是B1C1中点
已知:三棱柱ABC-A1B1C1中,A1A⊥平面ABC,CA=CB,D是AB的中点,E是B1C1中点