题目内容
7.已知函数$f(x)=\frac{1}{2}-{cos^2}x+\sqrt{3}sinxcosx$.(1)求f(x)单调递减区间;
(2)△ABC中,角A,B,C的对边a,b,c满足b2+c2-a2>bc,求f(A)的取值范围.
分析 (1)利用三角函数恒等变换的应用化简函数解析式可得f(x)=sin(2x-$\frac{π}{6}$),令2kπ+$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,k∈Z,解得f(x)的减区间.
(2)由已知利用余弦定理可得cosA>$\frac{1}{2}$,可得$0<A<\frac{π}{3}$,解得2A-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{π}{2}$),利用正弦函数的图象和性质即可得解取值范围.
解答 (本题满分为12分)
解:(1)∵$f(x)=\frac{1}{2}-{cos^2}x+\sqrt{3}sinxcosx$=$\frac{1}{2}$-$\frac{1+cos2x}{2}$+$\frac{\sqrt{3}}{2}$sin2x=sin(2x-$\frac{π}{6}$),…3分
∴2kπ+$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,k∈Z,解得:kπ+$\frac{π}{3}$≤x≤kπ+$\frac{5π}{6}$,k∈Z,
∴f(x)的减区间$[\frac{π}{3}+kπ,\frac{5π}{6}+kπ],k∈Z$…(6分)
(2)∵b2+c2-a2>bc,
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$>$\frac{bc}{2bc}$=$\frac{1}{2}$,
∴由题意可知$0<A<\frac{π}{3}$,可得:2A-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{π}{2}$).…(9分)
∴$f(A)∈(-\frac{1}{2},1)$…(12分)
点评 本题主要考查了三角函数恒等变换的应用,余弦定理,正弦函数的图象和性质的应用,考查了转化思想和数形结合思想,属于基础题.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案| A. | (0,2) | B. | [0,2] | C. | {0,2} | D. | {0,1,2} |
| A. | .$\frac{1}{3}{t^2}$ | B. | $\frac{{\sqrt{3}}}{3}t$. | C. | .$\frac{{\sqrt{2}}}{3}t$. | D. | .$\frac{1}{2}t$ |
| A. | $\begin{array}{l}\\ y={3^x}\end{array}$ | B. | y=(-3)x | C. | y=2x+1 | D. | y=x3 |
| x | -2 | -1 | 0 | 1 | 2 |
| y | 5 | 2 | 2 | 1 |
| A. | 3 | B. | 4 | C. | 5 | D. | 2 |
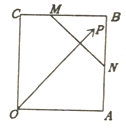 如图,已知正方形OABC边长为3,点M,N分别为线段BC,AB上一点,且2BM=MC,AN=NB,P为△BNM内一点(含边界),设$\overrightarrow{OP}=λ\overrightarrow{OA}+μ\overrightarrow{OC}$(λ,μ为实数),则$λ-\frac{1}{3}μ$的最大值为$\frac{5}{6}$.
如图,已知正方形OABC边长为3,点M,N分别为线段BC,AB上一点,且2BM=MC,AN=NB,P为△BNM内一点(含边界),设$\overrightarrow{OP}=λ\overrightarrow{OA}+μ\overrightarrow{OC}$(λ,μ为实数),则$λ-\frac{1}{3}μ$的最大值为$\frac{5}{6}$.