题目内容
3.设函数f(x)=lg[(2x-3)(x-1)]的定义域为集合A,函数$g(x)=\sqrt{-{x^2}+4ax-3{a^2}}$的定义域为集合B(其中a∈R,且a>0).(1)当a=1时求集合A∩B;
(2)当A∩B=B时,求实数a的取值范围.
分析 (1)根据对数函数的性质解关于x的不等式即可求出集合A,B,取交集即可;(2)根据集合的包含关系得到关于a的不等式组,解出即可.
解答 解:(1)由$(2x-3)(x-1)>0⇒x>\frac{3}{2}$或x<1,
∴$A=(-∞,1)∪(\frac{3}{2},+∞)$
当a=1时,由-x2+4x-3≥0⇒1≤x≤3,
∴B=[1,3],
∴$A∩B=(\frac{3}{2},3]$
(2)当a>0时B=[a,3a],
若A∩B=B⇒B⊆A,
∴$\left\{\begin{array}{l}a>0\\ 3a<1\end{array}\right.$或$a>\frac{3}{2}$,
解得$0<a<\frac{1}{3}$或$a>\frac{3}{2}$,
故a的取值范围是$(0,\frac{1}{3})∪(\frac{3}{2},+∞)$.
点评 本题考查了对数函数的性质,考查集合的运算,是一道基础题.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
13.已知平面上两点A(-a,0),B(a,0)(a>0),若圆(x-3)2+(y-4)2=4上存在点P,使得∠APB=90°,则a的取值范围是( )
| A. | [3,6] | B. | [3,7] | C. | [4,6] | D. | [0,7] |
14.已知空间向量$\vec a$=(1,n,2),$\vec b$=(-2,1,2),若2$\vec a$-$\vec b$与$\vec b$垂直,则|$\vec a$|等于( )
| A. | $\frac{5\sqrt{3}}{2}$ | B. | $\frac{3\sqrt{5}}{2}$ | C. | $\frac{\sqrt{37}}{2}$ | D. | $\frac{\sqrt{21}}{2}$ |
18.设等比数列{an}的前n项积为Pn,若P12=32P7,则a10的值是( )
| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
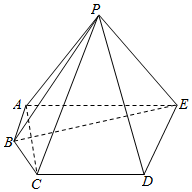 在五棱锥P-ABCDE中,平面PAE⊥平面ABCDE,△PAE为等腰直角三角形,且∠APE=90°,AB=2,AC=$\sqrt{10}$,AE=2AB,BE=2$\sqrt{5}$,DE=3,∠ABC=135°,AB∥DE
在五棱锥P-ABCDE中,平面PAE⊥平面ABCDE,△PAE为等腰直角三角形,且∠APE=90°,AB=2,AC=$\sqrt{10}$,AE=2AB,BE=2$\sqrt{5}$,DE=3,∠ABC=135°,AB∥DE