题目内容
函数y=x2(x>0)的图象在点(ak,ak2)处的切线与x轴交点的横坐标为ak+1,其中k∈N+,若a1=16,则a1+a3+a5=
21
21
.分析:由y=x2(x>0),求出y=x2(x>0)在点(ak,ak2)处的切线方程是2akx-y-ak2=0,再由切线与x轴交点的横坐标为ak+1,知ak+1=
ak,所以{an}是首项为a1=1,公比q=
的等比数列,
由此能求出a1+a3+a5.
| 1 |
| 2 |
| 1 |
| 2 |
由此能求出a1+a3+a5.
解答:解:∵y=x2(x>0),
∴y′=2x,
∴y=x2(x>0)在点(ak,ak2)处的切线方程是:
y-ak2=2ak(x-ak),
整理,得2akx-y-ak2=0,
∵切线与x轴交点的横坐标为ak+1,
∴ak+1=
ak,
∴{an}是首项为a1=1,公比q=
的等比数列,
∴a1+a3+a5=16+16×
+16×
=21.
故答案为:21.
∴y′=2x,
∴y=x2(x>0)在点(ak,ak2)处的切线方程是:
y-ak2=2ak(x-ak),
整理,得2akx-y-ak2=0,
∵切线与x轴交点的横坐标为ak+1,
∴ak+1=
| 1 |
| 2 |
∴{an}是首项为a1=1,公比q=
| 1 |
| 2 |
∴a1+a3+a5=16+16×
| 1 |
| 4 |
| 1 |
| 16 |
故答案为:21.
点评:本题考查数列与函数的综合,综合性强,难度大,容易出错.解题时要认真审题,注意导数、切线方程和等比数列性质的灵活运用.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
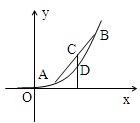 设a,b,λ都为正数,且a≠b,对于函数y=x2(x>0)图象上两点A(a,a2),B(b,b2).
设a,b,λ都为正数,且a≠b,对于函数y=x2(x>0)图象上两点A(a,a2),B(b,b2).