题目内容
6.已知tan(θ+$\frac{π}{2}$)=2,则sinθcosθ=-$\frac{2}{5}$.分析 利用诱导公式、同角三角函数的基本关系,求得要求式子的值.
解答 解:∵tan(θ+$\frac{π}{2}$)=-$\frac{1}{tanθ}$=2,∴tanθ=-$\frac{1}{2}$,
则sinθcosθ=$\frac{sinθ•cosθ}{{sin}^{2}θ{+cos}^{2}θ}$=$\frac{tanθ}{{tan}^{2}θ+1}$=-$\frac{2}{5}$,
故答案为:-$\frac{2}{5}$.
点评 本题主要考查诱导公式、同角三角函数的基本关系的应用,属于基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
17.已知数列{an}满足an+1=an-an-1(n≥2),a1=a,a2=b,设Sn=a1+a2+…+an,则下列结论正确的是( )
| A. | a100=-a S100=2b-a | B. | a100=-b S100=2b-a | ||
| C. | a100=-b S100=b-a | D. | a100=-a S100=b-a |
14.已知集合$A=\{x|\frac{x-2}{x+1}≤0,x∈Z\}$,B={1,2,3},则A∩B=( )
| A. | {1} | B. | {1,2} | C. | {0,1,2,3} | D. | {-1,0,1,2,3} |
18.阅读下面的程序框图,运行相应的程序,输出的结果为( )


| A. | -3 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | 2 |
15.函数f(x)=$\left\{\begin{array}{l}{f(x+3),x<3}\\{lo{g}_{2}(x-1),x≥3}\end{array}\right.$,则f(-1)的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
16.若某程序框图如图所示,则输出的p的值是( )
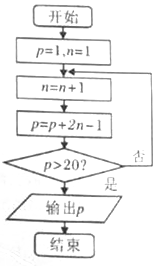

| A. | 49 | B. | 36 | C. | 25 | D. | 16 |
 在等腰Rt△ABC中,∠BAC=90°,腰长为2,D、E分别是边AB、BC的中点,将△BDE沿DE翻折,得到四棱锥B-ADEC,且F为棱BC中点,BA=$\sqrt{2}$.
在等腰Rt△ABC中,∠BAC=90°,腰长为2,D、E分别是边AB、BC的中点,将△BDE沿DE翻折,得到四棱锥B-ADEC,且F为棱BC中点,BA=$\sqrt{2}$.