题目内容
17.已知数列{an}满足an+1=an-an-1(n≥2),a1=a,a2=b,设Sn=a1+a2+…+an,则下列结论正确的是( )| A. | a100=-a S100=2b-a | B. | a100=-b S100=2b-a | ||
| C. | a100=-b S100=b-a | D. | a100=-a S100=b-a |
分析 数列{an}满足an+1=an-an-1(n≥2),a1=a,a2=b,可得:an+6=an,a100=a4=-a.即可得出.
解答 解:∵数列{an}满足an+1=an-an-1(n≥2),a1=a,a2=b,
∴a3=b-a,a4=-a,a5=-b,a6=a-b,a7=a,a8=b,…,
∴an+6=an,
∴a100=a4=-a.
设Sn=a1+a2+…+an,则S100=(a1+a2+a3+a4)+16(a1+…+a6)
=2b-a+16×(a+b+b-a-a-b+a-b)=2b-a,
故选:A.
点评 本题考查了数列递推关系、数列的周期性、数列求和,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
8.已知圆心为(2,-3),一条直径的两个端点恰好在两个坐标轴上,则圆的方程是( )
| A. | (x-2)2+(y+3)2=5 | B. | (x-2)2+(y+3)2=21 | C. | (x-2)2+(y+3)2=13 | D. | (x-2)2+(y+3)2=52 |
 已知定义在[-2,2]上的函数y=f(x)和 y=g(x),其图象如图所示:给出下列四个命题:
已知定义在[-2,2]上的函数y=f(x)和 y=g(x),其图象如图所示:给出下列四个命题: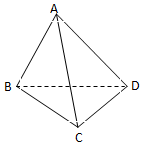 如图,在三棱锥A-BCD中,已知,∠BAC=60°,BD=DC=$\sqrt{2}$,AB=AC=AD=2.
如图,在三棱锥A-BCD中,已知,∠BAC=60°,BD=DC=$\sqrt{2}$,AB=AC=AD=2. 公元263年左右,我国数学家刘徽创立了“割圆术”,并利用“割圆术”得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的n值为(参考数据:$\sqrt{3}≈1.732$,sin15°≈0.2500,sin7.5°≈0.2588)( )
公元263年左右,我国数学家刘徽创立了“割圆术”,并利用“割圆术”得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的n值为(参考数据:$\sqrt{3}≈1.732$,sin15°≈0.2500,sin7.5°≈0.2588)( )