题目内容
4.对于集合M、N,定义M-N={x|x∈M且x∉N},M⊕N=(M-N)∪(N-M),设M={y|y=x2-4x,x∈R},N={y|y=-2x,x∈R},则M⊕N=[0,+∞)∪(-∞,-4).分析 由配方法和二次函数的性质求出M,由指数函数的性质求出N,由新定义和并集的运算求出(M-N)、(N-M)和M⊕N.
解答 解:由y=x2-4x=(x-2)2-4得,y≥-4,
则M={y|y=x2-4x,x∈R}=[-4,+∞),
由y=2x>0得,y=-2x<0,则N={y|y=-2x,x∈R}=(-∞,0),
∵M-N={x|x∈M且x∉N},∴M-N=[0,+∞),N-M=(-∞,-4),
∵M⊕N=(M-N)∪(N-M),
∴M⊕N=[0,+∞)∪(-∞,-4),
故答案为:[0,+∞)∪(-∞,-4).
点评 本题考查了集合新定义和并集的运算,以及二次函数、指数函数的性质,属于基础题.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
15.下列两个变量中,具有相关关系的是( )
| A. | 正方体的体积棱长 | B. | 匀速行驶的汽车的行驶距离与时间 | ||
| C. | 人的身高与体重 | D. | 人的身高与视力 |
12.已知集合P=$\{x|y=\sqrt{x+1}\}$,集合Q=$\{y|y=\sqrt{x+1}\}$,则P与Q的关系是( )
| A. | P=Q | B. | P⊆Q | C. | P?Q | D. | P∩Q=ϕ |
19.下列函数中既是奇函数,又在区间(-1,1)上是增函数的为( )
| A. | y=|x| | B. | y=2x | C. | y=x2 | D. | y=2x+1 |
13.某校共有17人获得北大、清华保送资格,具体人数如下:
若随机从获取北大、清华保送资格的学生中各取一名,则至少1人是参加数学竞赛的概率为( )
| 竞赛学科 | 数学 | 物理 | 化学 |
| 北大 | 6 | 4 | 2 |
| 清华 | 1 | 0 | 4 |
| A. | $\frac{1}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{15}{34}$ | D. | $\frac{91}{136}$ |
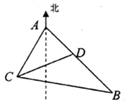 如图,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,则AC=24km.
如图,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,则AC=24km.