题目内容
5.设函数f(x)=kax-a-x(a>0且a≠1,k∈R),f(x)是定义域为R的奇函数.(1)求k的值;
(2)已知a=3,若f(3x)≥λ•f(x)对于x∈[1,2]时恒成立.请求出 最大的整数λ
分析 (1)由奇函数的性质f(0)=0得k=2;
(2)根据a=3,将f(3x)≥λ•f(x)表示出来,利用换元法和参变量分离法,将不等式转化为λ≤t2+3对t∈[$\frac{8}{3}$,$\frac{80}{9}$]恒成立,利用二次函数的性质,求得t2+3的最小值,即可求得λ的取值范围,从而得到答案.
解答 解:(1)由奇函数的性质f(0)=0得k=2
(2)由题意,即33x+3-3x≥λ(3x-3-x),在x∈[1,2]时恒成立
令t=3x-3-x,x∈[1,2],则t∈[$\frac{8}{3}$,$\frac{80}{9}$],
则(3x-3-x)(32x+3-2x+1)≥λ(3x-3-x),x∈[1,2]恒成立,
即为t(t2+3)≥λ•t,t∈[$\frac{8}{3}$,$\frac{80}{9}$]恒成立,
λ≤t2+3,t∈[$\frac{8}{3}$,$\frac{80}{9}$],恒成立,当t=$\frac{8}{3}$时,(t2+3)min=$\frac{91}{9}$,
∴λ≤$\frac{91}{9}$,则λ的最大整数为10.,则λ的最大整数为10.
点评 本题考查函数的性质,考查了函数的恒成立问题,对于函数的恒成立问题,一般选用参变量分离法、最值法、数形结合法进行求解.本题选用了参变量分离的方法转化成二次函数求最值问题.属于中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
15.下列两个变量中,具有相关关系的是( )
| A. | 正方体的体积棱长 | B. | 匀速行驶的汽车的行驶距离与时间 | ||
| C. | 人的身高与体重 | D. | 人的身高与视力 |
13.某校共有17人获得北大、清华保送资格,具体人数如下:
若随机从获取北大、清华保送资格的学生中各取一名,则至少1人是参加数学竞赛的概率为( )
| 竞赛学科 | 数学 | 物理 | 化学 |
| 北大 | 6 | 4 | 2 |
| 清华 | 1 | 0 | 4 |
| A. | $\frac{1}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{15}{34}$ | D. | $\frac{91}{136}$ |
20.下列命题:①如果x=y,则sinx=siny;②如果a>b,则a2>b2;③A,B是两个不同定点,动点P满足|PA|+|PB|是常数,则动点P的轨迹是椭圆.其中正确命题的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
10.已知函数f(x)=$\frac{1}{{\sqrt{2-x}}}+\sqrt{x+2}$的定义域为( )
| A. | {x|x≥-2} | B. | {x|x<2} | C. | {x|-2<x<2} | D. | {x|-2≤x<2} |
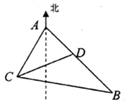 如图,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,则AC=24km.
如图,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,则AC=24km.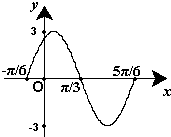 已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的 一段图象(如图)所示.
已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<π)的 一段图象(如图)所示.