题目内容
17.设F1,F2分别是椭圆$\frac{x^2}{4}+{y^2}$=1的左、右焦点.(1)若M是该椭圆上的一点,且∠F1MF2=120°,求△F1MF2的面积;
(2)若P是该椭圆上的一个动点,求$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}$的最大值和最小值.
分析 (1)由由椭圆标准方程:$\frac{x^2}{4}+{y^2}$=1,a=2,b=1,c2=a2-b2=3,求得F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),丨F1F2丨=2$\sqrt{3}$,由椭圆的定义可知:丨MF1丨+丨MF2丨=2a=4,由余弦定理可知:丨F1F2丨=丨MF1丨2+丨MF2丨2-2丨MF1丨•丨MF2丨cos∠F1MF2,代入即可求得丨MF1丨•丨MF2丨=4,由三角形的面积公式可知S=$\frac{1}{2}$×丨MF1丨•丨MF2丨×sin∠F1MF2,即可求得△F1MF2的面积;
(2)由(1)可知F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),设P (x,y),(-2≤x≤2),则$\overrightarrow{P{F}_{1}}$=(-$\sqrt{3}$-x,-y),$\overrightarrow{P{F}_{2}}$=($\sqrt{3}$-x,-y),根据向量数量积的坐标表示,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=$\frac{1}{4}$(3x2-8),由x的取值范围,当x=0,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$有最小值-2; 当x=±2,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$有最大值1.
解答 解:(1)由椭圆标准方程:$\frac{x^2}{4}+{y^2}$=1,a=2,b=1,c2=a2-b2=3,
∴F1(-$\sqrt{3}$,0),F2($\sqrt{3}$,0),
∴丨F1F2丨=2$\sqrt{3}$,又M是该椭圆上的一点,
∴丨MF1丨+丨MF2丨=2a=4,
∵∠F1MF2=120°,
∴在△F1MF2中,由余弦定理可知:丨F1F2丨=丨MF1丨2+丨MF2丨2-2丨MF1丨•丨MF2丨cos∠F1MF2,
∴(2$\sqrt{3}$)2=4-丨MF1丨•丨MF2丨,解得:丨MF1丨•丨MF2丨=4,
∴△F1MF2的面积为S=$\frac{1}{2}$×丨MF1丨•丨MF2丨×sin∠F1MF2=$\frac{1}{2}$×4×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
△F1MF2的面积$\sqrt{3}$;
(2)设P (x,y),(-2≤x≤2),$\overrightarrow{P{F}_{1}}$=(-$\sqrt{3}$-x,-y),$\overrightarrow{P{F}_{2}}$=($\sqrt{3}$-x,-y),
则$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=(-$\sqrt{3}$-x,-y)($\sqrt{3}$-x,-y)=x2+y2-3=x2+1-$\frac{{x}^{2}}{4}$-3=$\frac{1}{4}$(3x2-8),
∵-2≤x≤2,
∴当x=0,即点P为椭圆短轴端点时,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$有最小值-2;
当x=±2,即点P为椭圆长轴端点时,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$有最大值1.
点评 本题考查椭圆的焦点三角形的面积公式,考查余弦定理的应用,向量数量积的坐标表示,考查二次函数的性质,考查计算能力,属于中档题.

| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
| A. | 3 | B. | (3,0) | C. | 4 | D. | (4,0) |
| A. | 2 | B. | 4 | C. | 5 | D. | 2$\sqrt{13}$ |
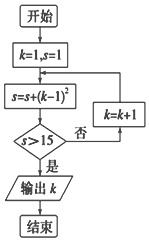
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
| A. | (-3,0)∪(2,3) | B. | (-∞,-3)∪(0,3) | C. | (-∞,-3)∪(3,+∞) | D. | (-3,0)∪(2,+∞) |