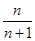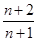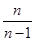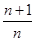题目内容
设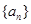 是公比大于1的等比数列,
是公比大于1的等比数列,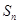 为数列
为数列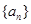 的前
的前 项和.已知
项和.已知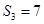 ,且
,且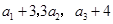 构成等差数列.
构成等差数列.
(1)求数列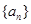 的通项公式.
的通项公式.
(2)令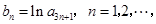 求数列
求数列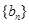 的前
的前 项和
项和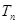 .
.
(1) ;(2)
;(2) .
.
解析试题分析:由已知得
解得 .
.
设数列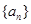 的公比为
的公比为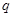 ,由
,由 ,可得
,可得 .
.
又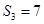 ,可知
,可知 ,即
,即 ,
,
解得
由题意得
 .
.
故数列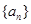 的通项为
的通项为 .
.
(2)由于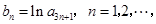
由(1)得

又
 是等差数列.
是等差数列.

故 .
.
考点:本题主要考查等比数列的通项公式,等差数列的通项公式、前n项求和公式。
点评:基础题,各项为正的等比数列,取对数后得到等差数列,这一结论可指导我们找到解题思路。

练习册系列答案
相关题目
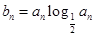 ,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的正整数n的最小值.
,Sn=b1+b2+…+bn,求使Sn+n·2n+1>50成立的正整数n的最小值.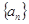 中,已知
中,已知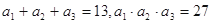 ,且公比为正整数.
,且公比为正整数. 的通项公式;(5分)
的通项公式;(5分) 项和.(5分)
项和.(5分)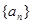 是公差不为零的等差数列,
是公差不为零的等差数列, 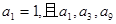 成等比数列.
成等比数列.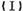 求数列
求数列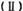 求数列
求数列 的前n项和
的前n项和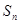
 的相邻两项
的相邻两项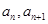 是关于
是关于 的方程
的方程 的两根,且
的两根,且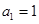
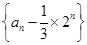 是等比数列;
是等比数列; 项和
项和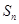 ;
;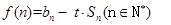 若
若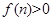 对任意的
对任意的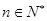 都成立,求
都成立,求 的取值范围。
的取值范围。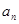 }的前n 项和为
}的前n 项和为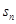 ,已知
,已知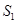 ,
,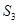 ,
,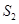 成等差数列
成等差数列 -
-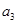 =3,求
=3,求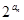 +2n,求数列{bn}的前n项和Tn.
+2n,求数列{bn}的前n项和Tn. 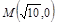 作直线
作直线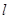 交曲线
交曲线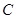 :
: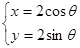 (
(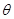 为参数)于
为参数)于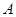 、
、 两点,若
两点,若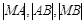 成等比数列,求直线
成等比数列,求直线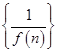 (n∈N*)的前n项和是( )
(n∈N*)的前n项和是( )