题目内容
已知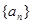 是公差不为零的等差数列,
是公差不为零的等差数列, 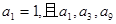 成等比数列.
成等比数列. 求数列
求数列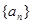 的通项;
的通项; 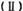 求数列
求数列 的前n项和
的前n项和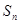
(1) (2)
(2)
解析试题分析:解(1)由题设知公差
由 成等比数列得
成等比数列得
解得 (舍去)
(舍去)
故 的通项
的通项

由等比数列前n项和公式得
考点:等比数列,等差数列
点评:解决该试题的关键是利用等差数列和和等比中项来求解通项公式,同时得到数列的和,属于基础题。

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
已知数列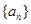 的前n项和为
的前n项和为 ,且
,且 ,则
,则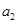 =
=
| A.4 | B.2 | C.1 | D.-2 |
 中,
中, ,
, (
( 是常数,
是常数, ),且
),且 成公比不为
成公比不为 的等比数列.
的等比数列.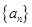 中,
中,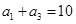 ,
,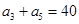 .设
.设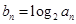 .
. 的通项公式;
的通项公式;  ,
,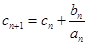 ,求证:
,求证: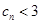 ;
;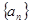 的各项均为正数,Sn为其前n项和,对于任意
的各项均为正数,Sn为其前n项和,对于任意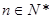 ,满足关系
,满足关系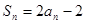 .
. 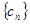 中,设
中,设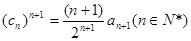 ,求数列
,求数列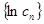 中的最大项.
中的最大项. 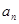 }的前n项和为
}的前n项和为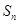 ,且
,且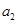 =3,
=3,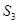 =13,数列{
=13,数列{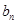 }满足
}满足 =
=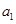 ,点P(
,点P(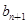 )在直线x-y+2=0上,n∈N﹡.
)在直线x-y+2=0上,n∈N﹡.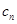 =
=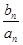 ,数列{
,数列{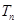 ,若
,若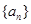 是公比大于1的等比数列,
是公比大于1的等比数列,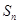 为数列
为数列 项和.已知
项和.已知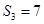 ,且
,且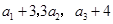 构成等差数列.
构成等差数列.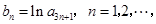 求数列
求数列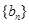 的前
的前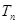 .
.  为等比数列,且首项为
为等比数列,且首项为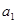 ,公比为
,公比为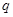 ,前
,前 项和为
项和为 .
.