题目内容
(本小题10分) 等比数列{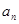 }的前n 项和为
}的前n 项和为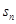 ,已知
,已知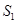 ,
,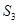 ,
,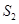 成等差数列
成等差数列
(1)求{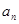 }的公比q;
}的公比q;
(2)求 -
-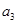 =3,求
=3,求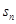 ;
;
(1)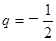 ;(2)
;(2)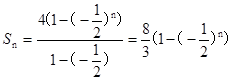 。
。
解析试题分析:(1)依题意有 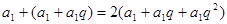 ,由于
,由于 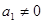 ,故
,故 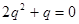 ,故可得公比的值。
,故可得公比的值。
(2)由已知可得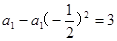 ,从而得到首项的值,并求解和式。
,从而得到首项的值,并求解和式。
(1)依题意有 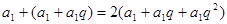
由于 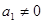 ,故
,故 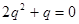
又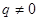 ,从而
,从而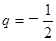 5分
5分
(2)由已知可得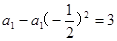
故
从而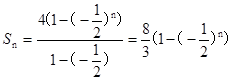 10分
10分
考点:本题主要考查等比数列和等差数列的通项公式以及前n项和的关系式的求解运用。
点评:解决该试题的关键是数量的运用等差数列和等比数列的前n项和公式得到基本量的关系式,进而得到结论。

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
已知数列 的通项公式为
的通项公式为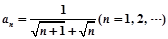 ,
,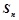 是数列
是数列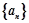 的前n项和,则
的前n项和,则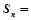 ( )
( )
A.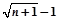 | B.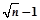 | C.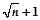 | D.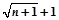 |
 的首项为
的首项为 ,前
,前 项和为
项和为 ,且
,且 是
是 与
与 的等差中项
的等差中项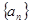 的各项均为正数,Sn为其前n项和,对于任意
的各项均为正数,Sn为其前n项和,对于任意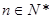 ,满足关系
,满足关系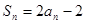 .
. 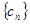 中,设
中,设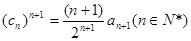 ,求数列
,求数列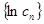 中的最大项.
中的最大项. 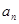 }的前n项和为
}的前n项和为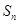 ,且
,且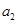 =3,
=3,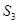 =13,数列{
=13,数列{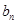 }满足
}满足 =
=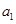 ,点P(
,点P(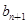 )在直线x-y+2=0上,n∈N﹡.
)在直线x-y+2=0上,n∈N﹡.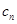 =
=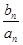 ,数列{
,数列{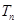 ,若
,若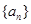 是公比大于1的等比数列,
是公比大于1的等比数列,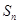 为数列
为数列 项和.已知
项和.已知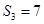 ,且
,且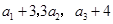 构成等差数列.
构成等差数列.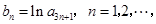 求数列
求数列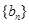 的前
的前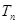 .
. 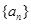 中,
中, .
.  分别为等差数列
分别为等差数列 的第4项和第16项,求数列
的第4项和第16项,求数列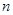 项和
项和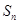 .
. 为等比数列,且首项为
为等比数列,且首项为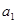 ,公比为
,公比为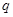 ,前
,前 项和为
项和为 .
.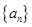 中,
中,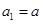 ,
, ,
,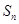 是数列
是数列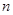 项和,且
项和,且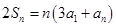 ,
,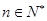 .
.  的值;
的值;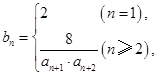
 是数列
是数列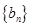 的前
的前