题目内容
17．将函数y=sinx+cosx图象上各点的横坐标缩短到原来的$\frac{1}{2}$倍，得到y=f（x）的图象，则y=f（x）的最小正周期为（ ）| A． | $\frac{π}{2}$ | B． | π | C． | 2π | D． | 4π |
分析 求出y=f（x）的解析式，即可求出y=f（x）的最小正周期．
解答 解：y=sinx+cosx=$\sqrt{2}$sin（x+$\frac{π}{4}$），横坐标缩短到原来的$\frac{1}{2}$倍，得到y=f（x）=$\sqrt{2}$sin（2x+$\frac{π}{4}$），
T=$\frac{2π}{2}$=π，
故选B．
点评 本题考查y=f（x）的最小正周期，考查图象变换，确定函数的解析式是关键．
练习册系列答案
相关题目
8．下列说法正确的是（ ）
| A． | 若命题p：?x0∈R，x02-x0+1＜0，则￢p：?x∉R，x2-x+1≥0 | |
| B． | 已知相关变量（x，y）满足回归方程$\stackrel{∧}{y}$=2-4x，若变量x增加一个单位，则y平均增加4个单位 | |
| C． | 命题“若圆C：（x-m+1）2+（y-m）2=1与两坐标轴都有公共点，则实数m∈[0，1]为真命题 | |
| D． | 已知随机变量X～N（2，σ2），若P（X＜a）=0.32，则P（X＞4-a）=0.68 |
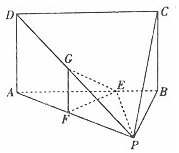在四棱锥P-ABCD中，底面ABCD为矩形，平面PAB⊥平面ABCD，AB=AP=3，AD=PB=2，E为线段AB上一点，且AE：EB=7：2，点F、G分别为线段PA、PD的中点．
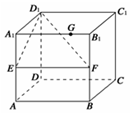在棱长为1的正方体ABCD-A1B1C1D1中，E、F分别为棱AA1、BB1的中点，G为棱A1B1上的一点，且A1G=λ（0≤λ≤1），则点G到平面D1EF的距离为$\frac{{\sqrt{5}}}{5}$．