题目内容
10.若F(c,0)为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的右焦点,过F点作该双曲线的一条渐近线的垂线与两条渐近线交于A、B两点,△AOB的面积为$\frac{12{a}^{2}}{7}$,则该双曲线的离心率为$\frac{5}{4}$.分析 求出双曲线的渐近线方程,设两条渐近线的夹角为θ,由两直线的夹角公式,可得tanθ=tan∠AOB,求出F到渐近线y=$\frac{b}{a}$x的距离为b,即有|OB|=a,△OAB的面积可以表示为$\frac{1}{2}$•a•atanθ,结合条件可得a,b的关系,再由离心率公式即可计算得到.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的渐近线方程为y=±$\frac{b}{a}$x,
设两条渐近线的夹角为θ,
则tanθ=tan∠AOB=$\frac{\frac{b}{a}-(-\frac{b}{a})}{1+\frac{b}{a}•(-\frac{b}{a})}$=$\frac{2ab}{{a}^{2}-{b}^{2}}$,
设FB⊥OB,则F到渐近线y=$\frac{b}{a}$x的距离为d=$\frac{|bc|}{\sqrt{{a}^{2}+{b}^{2}}}$=b,
即有|OB|=a,
则△OAB的面积可以表示为$\frac{1}{2}$•a•atanθ=$\frac{{a}^{3}b}{{a}^{2}-{b}^{2}}$=$\frac{12{a}^{2}}{7}$,
解得$\frac{b}{a}$=$\frac{3}{4}$,
则e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\frac{5}{4}$.
故答案为:$\frac{5}{4}$.
点评 本题主要考查双曲线的几何性质,结合着较大的运算量,属于中档题.

练习册系列答案
相关题目
18.一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了10次试验,收集数据如下:
(1)画出散点图;
(2)求回归方程;
(3)关于加工零件的个数与加工时间,你能得出什么结论?
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| 加工时间y(min) | 62 | 68 | 75 | 81 | 89 | 95 | 102 | 108 | 115 | 122 |
(2)求回归方程;
(3)关于加工零件的个数与加工时间,你能得出什么结论?
1.已知集合A={x|$\frac{1}{x}$<1},B={y|y=2-x-1,x∈R},则A∩B=( )
| A. | ∅ | B. | {x|x>1} | C. | {x|-1<x<0} | D. | {x|-1<x<0或x>1} |
18.已知函数g(x)=$\left\{\begin{array}{l}{\frac{1}{x+1}-3,-1<x≤0}\\{{x}^{2}-3x+2,0<x≤1}\end{array}\right.$,若方程g(x)-mx-m=0有且仅有两个不等的实根,则实数m的取值范围是( )
| A. | (-$\frac{9}{4}$,-2]∪[0,2] | B. | (-$\frac{11}{4}$,-2]∪[0,2] | C. | (-$\frac{9}{4}$,-2]∪[0,2) | D. | (-$\frac{11}{4}$,-2]∪[0,2) |
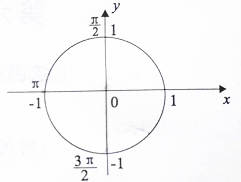 单位圆上三角函数值的集合解释是“角在弧上,值在线上”,试在图中画出α属于第Ⅲ象限的一个正弦值,余弦值.
单位圆上三角函数值的集合解释是“角在弧上,值在线上”,试在图中画出α属于第Ⅲ象限的一个正弦值,余弦值.