题目内容
1.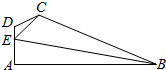 如图所示,在平面四边形ABCD中,AB⊥AD,∠ADC=$\frac{2π}{3}$,E为AD边上一点,CE=$\sqrt{7}$,DE=1,AE=2,∠BEC=$\frac{π}{3}$.
如图所示,在平面四边形ABCD中,AB⊥AD,∠ADC=$\frac{2π}{3}$,E为AD边上一点,CE=$\sqrt{7}$,DE=1,AE=2,∠BEC=$\frac{π}{3}$.(Ⅰ)求sin∠CED的值;
(Ⅱ)求BE的长.
分析 (1)在△CDE中,使用余弦定理解出CD,再利用正弦定理求出sin∠CED;
(2)利用诱导公式与和角公式求出sin∠AEB,再在Rt△ABE中解出BE.
解答 解:(1)在△CDE中,由余弦定理得CE2=DE2+CD2-2DE•CDcos$\frac{2π}{3}$,即7=1+CD2+CD,解得CD=2.
由正弦定理得$\frac{CD}{sin∠CED}=\frac{CE}{sin∠CDE}$,即$\frac{2}{sin∠CED}=\frac{\sqrt{7}}{\frac{\sqrt{3}}{2}}$,解得sin∠CED=$\frac{\sqrt{21}}{7}$.
(2)∵sin∠CED=$\frac{\sqrt{21}}{7}$,∴cos∠CED=$\frac{2\sqrt{7}}{7}$.
∴sin∠AEB=sin(∠CED+60°)=$\frac{\sqrt{21}}{7}×\frac{1}{2}$+$\frac{2\sqrt{7}}{7}×\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{21}}{14}$.∴cos∠AEB=$\frac{\sqrt{7}}{14}$.
∵cos∠AEB=$\frac{AE}{BE}$,∴BE=$\frac{AE}{sin∠AEB}$=4$\sqrt{7}$.
点评 本题考查了正余弦定理在解三角形中的应用,是中档题.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
9.抛物线y=$\frac{1}{8}$x2上一点M到焦点的距离为4,则点M的纵坐标为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
6.在如图所示的程序框图中,当输出的T的值最大时,正整数k的值等于( )


| A. | 6 | B. | 7 | C. | 6或7 | D. | 8 |