题目内容
16.函数g(x)=$\left\{\begin{array}{l}{0,x=0}\\{lo{g}_{2}|x|,x≠0}\end{array}\right.$,f(x)=x2-2x,若关于x的方程f(g(x))-a=0有四个不同的实数解,则实数a的取值范围是(-1,0)∪(0,+∞).分析 利用换元法设t=g(x),作出计算g(x)的图象,结合一元二次函数的图象和性质,利用数形结合进行求解即可.
解答 解:设t=g(x),
作出函数g(x)的图象如图: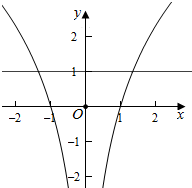
则当t=0时,方程t=g(x)有三个不同的根,
当t≠0时,方程t=g(x)有2个不同的根,
若则关于x的方程f(g(x))-a=0有四个不同的实数解,
等价为f(t)=a有2个不等于0的不同的实数解,
∵f(x)=x2-2x=(x-1)2-1≥-1,
∴a>0,或-1<a<0,
故实数a的取值范围是(-1,0)∪(0,+∞),
故答案为:(-1,0)∪(0,+∞)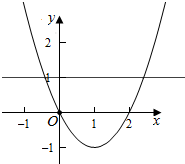
点评 本题主要考查函数与方程的应用,利用换元法以及数形结合是解决本题的关键.

练习册系列答案
相关题目
6.已知全集U={0,1,2,3,4},集合A={1,2},B={2,3,4},则(∁UA)∩B( )
| A. | {1} | B. | {2} | C. | {3,4} | D. | {1,2,3,4} |
7.下列函数在其定义域内,既是奇函数又是增函数的为( )
| A. | y=-$\frac{1}{x}$ | B. | y=ln(x+5) | C. | y=x2-1 | D. | y=x|x| |
11.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格试销,得到如下数据:
由表中数据,求的线性回归方程$\widehat{y}$=-2x+10.6,则表中m的值为( )
| 单价x(元) | 4.4 | 4.1 | 3.6 | 3.2 | 2.7 | 1.8 |
| 销量y(千件) | 1.6 | 2 | m | 4.8 | 5.2 | 6 |
| A. | 4.2 | B. | 4.4 | C. | 4.6 | D. | 4.7 |
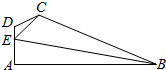 如图所示,在平面四边形ABCD中,AB⊥AD,∠ADC=$\frac{2π}{3}$,E为AD边上一点,CE=$\sqrt{7}$,DE=1,AE=2,∠BEC=$\frac{π}{3}$.
如图所示,在平面四边形ABCD中,AB⊥AD,∠ADC=$\frac{2π}{3}$,E为AD边上一点,CE=$\sqrt{7}$,DE=1,AE=2,∠BEC=$\frac{π}{3}$.