题目内容
给出下列命题:
①函数y=x-1,y=x
,y=(x-1)2,y=x3中,有三个函数在区间(0,+∞)上单调递增;
②若logm3<logn3<0,则0<n<m<1;
③已知函数f(x)=
,那么方程f(x)=
有两个实数根.
其中正确命题的个数为( )
①函数y=x-1,y=x
| 1 |
| 2 |
②若logm3<logn3<0,则0<n<m<1;
③已知函数f(x)=
|
| 1 |
| 2 |
其中正确命题的个数为( )
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:计算题,作图题,函数的性质及应用
分析:①利用指数函数与幂函数的单调性,对y=x-1、y=(x-1)2、y=x
与y=x3四个函数在区间(0,+∞)上单调性逐个分析即可;
②利用对数函数的性质,结合图象法分析即可;
③在同一直角坐标系中,作出函数f(x)=
与y=
的图象,观察即可得到结论.
| 1 |
| 2 |
②利用对数函数的性质,结合图象法分析即可;
③在同一直角坐标系中,作出函数f(x)=
|
| 1 |
| 2 |
解答:
解:①∵y=x-1在区间(0,+∞)上单调递减,y=(x-1)2在[0,1]上单调递减,在[1,+∞)上单调递增,y=x
与y=x3两个函数在区间(0,+∞)上单调递增,
故①错误;
②∵logm3<logn3<0,

∴0<m<1,0<n<1且n<m,
即0<n<m<1,故②正确;
③∵f(x)=
,其图形如下:
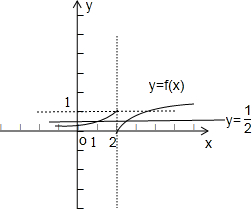
由图知,方程f(x)=
有两个实数根,故③正确,
综上所述,正确命题的个数为2个.
故选:C.
| 1 |
| 2 |
故①错误;
②∵logm3<logn3<0,

∴0<m<1,0<n<1且n<m,
即0<n<m<1,故②正确;
③∵f(x)=
|
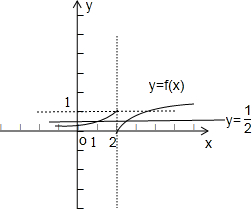
由图知,方程f(x)=
| 1 |
| 2 |
综上所述,正确命题的个数为2个.
故选:C.
点评:本题考查命题的真假判断与应用,着重考查函数的单调性与图象的综合应用,考查作图与分析、运算的能力,属于难题.

练习册系列答案
相关题目
设集合M={x∈N|x2+x-6<0},P={x|(x-1)(x-3)≤0},则M∩P=( )
| A、[1,2) | B、[1,2] |
| C、{1,2} | D、{1} |
已知函数f(x)在其定义域D上是单调函数,其值域为M,则下列说法中,错误的个数是( )
①若x0∈D,则有唯一的f(x0)∈M
②若f(x0)∈M,则有唯一的x0∈D
③对任意实数a,至少存在一个x0∈D,使得f(x0)=a
④对任意实数a,至多存在一个x0∈D,使得f(x0)=a.
①若x0∈D,则有唯一的f(x0)∈M
②若f(x0)∈M,则有唯一的x0∈D
③对任意实数a,至少存在一个x0∈D,使得f(x0)=a
④对任意实数a,至多存在一个x0∈D,使得f(x0)=a.
| A、1个 | B、2个 | C、3个 | D、4个 |
下列命题中真命题的是( )
| A、“关于x的不等式f(x)>0有解”的否定是“?x0∈R,使得f(x0)<0成立” |
| B、?x0∈R,使得ex0≤0成立 |
| C、?x∈R,3x>x3 |
| D、“x>a2+b2”是“x>2ab”的充分条件 |