题目内容
已知数列 中
中 ,数列
,数列 中
中 ,其中
,其中
(1)求证:数列 是等差数列
是等差数列
(2)设 是数列
是数列 的前n项和,求
的前n项和,求
(3)设 是数列
是数列 的前n 项和,求证:
的前n 项和,求证:
解:(1) , 而
, 而  ,
,
∴  .
.
∴ { }是首项为
}是首项为 ,公差为1的等差数列
,公差为1的等差数列
(2)由(1)可知 ,
,
 ,
,
于是 =
=
故有
 =6
=6
(3)证明:由(1)可知 
 ,
,
则

则 ++
++
 ,
,
∴

【解析】
试题分析:(1)由条件可得到  ,由此证得结论
,由此证得结论
(2)由(1) =
= ,用裂项法求出
,用裂项法求出 的值.
的值.
(3)由(1)可知  =
= ,求出Tn的解析式,可得
,求出Tn的解析式,可得 Tn 的解析式,用错位相减法求出Tn的解析式,从而可得要证的不等式成立.
Tn 的解析式,用错位相减法求出Tn的解析式,从而可得要证的不等式成立.
考点:数列与不等式的综合。

练习册系列答案
相关题目
 等于( )
等于( )
 (B)
(B)
 (D)
(D)
 的外接圆的圆心为
的外接圆的圆心为 ,满足:
,满足: ,
, ,且
,且 ,
, ,则
,则 ( )
( ) D.
D.
 B.
B.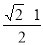 C. 1 D.
C. 1 D.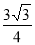
 的边长为
的边长为 ,
, ,点
,点 ,
, 分别在边
分别在边 、
、 上,
上, ,
, .若
.若 ,则
,则 的值为_____________
的值为_____________  ,
, ,
, ,则
,则 的大小关系是( )
的大小关系是( )  B.
B. C.
C. D.
D.
 )如图所示,则该几何体的侧面积为
)如图所示,则该几何体的侧面积为  .
.
 cm ,短轴长 ,离心率为 .
cm ,短轴长 ,离心率为 .