题目内容
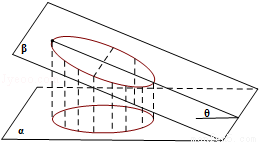
底面直径为12cm的圆柱被与底面成30°的平面所截,截口是一个椭圆,该椭圆的长轴长 8 cm ,短轴长 ,离心率为 .
cm ,短轴长 ,离心率为 .

8 cm,12cm,
cm,12cm,
【解析】
试题分析:根据平面与圆柱面的截线及椭圆的性质,可得圆柱的底面直径为12cm,截面与底面成30°,根据截面所得椭圆长轴、短轴与圆柱直径的关系,我们易求出椭圆的长轴长和短轴长,进而得到椭圆的离心率.
【解析】
∵圆柱的底面直径d为12cm,截面与底面成30°
∴椭圆的短轴长2b=d=12cm
椭圆的长轴长2a= =8
=8 cm
cm
根据 得,椭圆的半焦距长C=2
得,椭圆的半焦距长C=2 cm
cm
则椭圆的离心率e= =
= =
=
故答案为:8 cm,12cm,
cm,12cm,

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 中
中 ,数列
,数列 中
中 ,其中
,其中
 是等差数列
是等差数列 是数列
是数列 的前n项和,求
的前n项和,求
 是数列
是数列 的前n 项和,求证:
的前n 项和,求证:
 ,集合
,集合 ,
, ,则
,则 等于
等于 B.
B. C.
C. D.
D.
 中,
中, ,且对任意的正整数
,且对任意的正整数 都有
都有 ,则若
,则若 时,
时, _________.
_________.
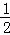 B.
B.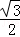 C.
C.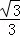 D.
D.
 (sinx﹣cosx)的导函数为f′(x),则下列结论正确的是( )
(sinx﹣cosx)的导函数为f′(x),则下列结论正确的是( )