题目内容
(本小题满分12分)
如果两个椭圆的离心率相等,那么就称这两个椭圆相似.已知椭圆 与椭圆
与椭圆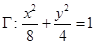 相似,且椭圆
相似,且椭圆 的一个短轴端点是抛物线
的一个短轴端点是抛物线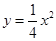 的焦点.
的焦点.
(Ⅰ)试求椭圆 的标准方程;
的标准方程;
(Ⅱ)设椭圆 的中心在原点,对称轴在坐标轴上,直线
的中心在原点,对称轴在坐标轴上,直线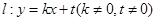 与椭圆
与椭圆 交于
交于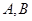 两点,且与椭圆
两点,且与椭圆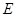 交于
交于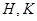 两点.若线段
两点.若线段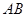 与线段
与线段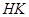 的中点重合,试判断椭圆
的中点重合,试判断椭圆 与椭圆
与椭圆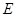 是否为相似椭圆?并证明你的判断.
是否为相似椭圆?并证明你的判断.
如果两个椭圆的离心率相等,那么就称这两个椭圆相似.已知椭圆
 与椭圆
与椭圆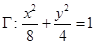 相似,且椭圆
相似,且椭圆 的一个短轴端点是抛物线
的一个短轴端点是抛物线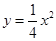 的焦点.
的焦点.(Ⅰ)试求椭圆
 的标准方程;
的标准方程;(Ⅱ)设椭圆
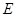 的中心在原点,对称轴在坐标轴上,直线
的中心在原点,对称轴在坐标轴上,直线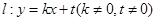 与椭圆
与椭圆 交于
交于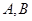 两点,且与椭圆
两点,且与椭圆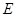 交于
交于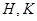 两点.若线段
两点.若线段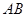 与线段
与线段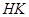 的中点重合,试判断椭圆
的中点重合,试判断椭圆 与椭圆
与椭圆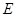 是否为相似椭圆?并证明你的判断.
是否为相似椭圆?并证明你的判断.(Ⅰ) .(Ⅱ)椭圆
.(Ⅱ)椭圆 与椭圆
与椭圆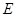 是相似椭圆. 证明见解析。
是相似椭圆. 证明见解析。
 .(Ⅱ)椭圆
.(Ⅱ)椭圆 与椭圆
与椭圆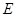 是相似椭圆. 证明见解析。
是相似椭圆. 证明见解析。试题分析:(Ⅰ)椭圆
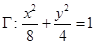 的离心率为
的离心率为 , 抛物线
, 抛物线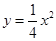 的焦点为
的焦点为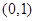 .
. 设椭圆
 的方程为
的方程为 ,由题意,得:
,由题意,得: 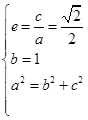 ,解得
,解得 ,
,∴椭圆
 的标准方程为
的标准方程为  . ………………………………4分
. ………………………………4分(Ⅱ)解法一:椭圆
 与椭圆
与椭圆 是相似椭圆. ………………………………5分
是相似椭圆. ………………………………5分联立
 和
和 的方程,
的方程, ,消去
,消去 ,得
,得 , ……6分
, ……6分设
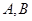 的横坐标分别为
的横坐标分别为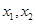 ,则
,则 .
. 设椭圆
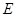 的方程为
的方程为 , …………………………………7分
, …………………………………7分联立方程组
 ,消去
,消去 ,得
,得 ,
,设
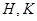 的横坐标分别为
的横坐标分别为 ,则
,则 .
. ∵弦
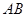 的中点与弦
的中点与弦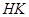 的中点重合,∴
的中点重合,∴
 ,
,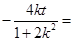
 ,
,∵
 ,∴化简得
,∴化简得 , ……………………………10分
, ……………………………10分求得椭圆
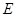 的离心率
的离心率 , ………………………12分
, ………………………12分∴椭圆
 与椭圆
与椭圆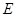 是相似椭圆.
是相似椭圆.解法二:(参照解法1评分)
设椭圆
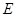 的方程为
的方程为 ,
, .
.∵
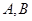 在椭圆
在椭圆 上,∴
上,∴ 且
且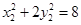 ,两式相减并恒等变形得
,两式相减并恒等变形得 .
. 由
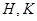 在椭圆
在椭圆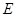 上,仿前述方法可得
上,仿前述方法可得 .
.∵弦
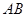 的中点与弦
的中点与弦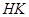 的中点重合,
的中点重合,∴
 ,求得椭圆
,求得椭圆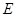 的离心率
的离心率 , 即椭圆
, 即椭圆 与椭圆
与椭圆 是相似椭圆.
是相似椭圆.点评:综合题,判断椭圆
 与椭圆
与椭圆 是否为相似椭圆,主要是要把握好“如果两个椭圆的离心率相等,那么就称这两个椭圆相似”这一定义,“点差法”是常用方法.
是否为相似椭圆,主要是要把握好“如果两个椭圆的离心率相等,那么就称这两个椭圆相似”这一定义,“点差法”是常用方法.
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 )在椭圆上,。
)在椭圆上,。 ,求△OAB的面积的取值范围。
,求△OAB的面积的取值范围。 ,过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.
,过焦点且垂直于长轴的弦长为1,且焦点与短轴两端点构成等边三角形.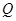
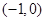 的直线
的直线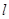 交椭圆于
交椭圆于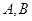 两点,交直线
两点,交直线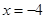 于点
于点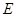 ,且
,且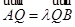 ,
,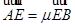 ,
,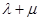 为定值,并计算出该定值.
为定值,并计算出该定值.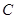 :
: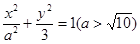 的右焦点
的右焦点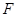 在圆
在圆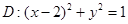 上,直线
上,直线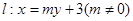 交椭圆于
交椭圆于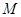 、
、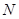 两点.
两点.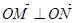 (
( 为坐标原点),求
为坐标原点),求 的值;
的值; 轴上的椭圆
轴上的椭圆 的离心率是
的离心率是 ,则
,则 的值为 ( )
的值为 ( )

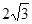

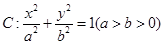 过点
过点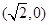 ,且离心率为
,且离心率为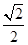 .
. 的方程;
的方程; 为椭圆
为椭圆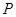 是椭圆
是椭圆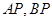 分别交直线
分别交直线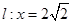 于
于 两点.
两点. 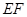 为直径的圆恒过
为直径的圆恒过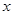 轴上的定点.
轴上的定点.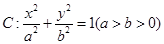 ,
,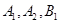 是椭圆
是椭圆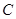 的顶点,若椭圆
的顶点,若椭圆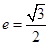 ,且过点
,且过点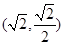 .
.
 ,使得
,使得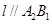 ,且与椭圆
,且与椭圆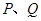 两点(异于椭圆
两点(异于椭圆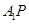 和直线
和直线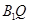 的倾斜角分别是
的倾斜角分别是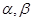 ,求证:
,求证: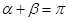 .
.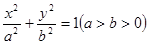 的顶点与焦点,若∠ ABC=90°,则该椭圆的离心率为 ( )
的顶点与焦点,若∠ ABC=90°,则该椭圆的离心率为 ( )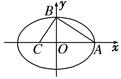


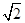 -1
-1 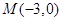 ,点
,点 ,动点
,动点 满足
满足 ,则点
,则点