题目内容
(本小题满分14分)
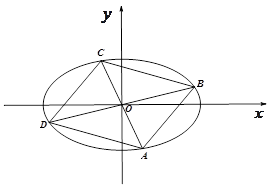
如图,已知椭圆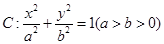 ,
,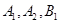 是椭圆
是椭圆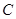 的顶点,若椭圆
的顶点,若椭圆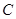 的离心率
的离心率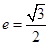 ,且过点
,且过点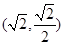 .
.
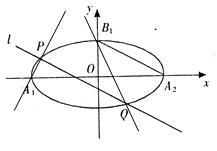
(Ⅰ)求椭圆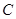 的方程;
的方程;
(Ⅱ)作直线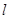 ,使得
,使得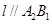 ,且与椭圆
,且与椭圆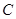 相交于
相交于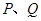 两点(异于椭圆
两点(异于椭圆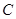 的顶点),设直线
的顶点),设直线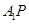 和直线
和直线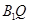 的倾斜角分别是
的倾斜角分别是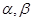 ,求证:
,求证: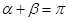 .
.
如图,已知椭圆
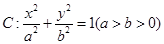 ,
,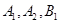 是椭圆
是椭圆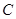 的顶点,若椭圆
的顶点,若椭圆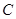 的离心率
的离心率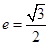 ,且过点
,且过点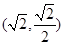 .
.
(Ⅰ)求椭圆
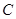 的方程;
的方程;(Ⅱ)作直线
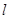 ,使得
,使得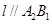 ,且与椭圆
,且与椭圆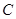 相交于
相交于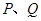 两点(异于椭圆
两点(异于椭圆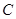 的顶点),设直线
的顶点),设直线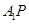 和直线
和直线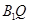 的倾斜角分别是
的倾斜角分别是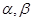 ,求证:
,求证: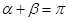 .
.(Ⅰ)  (Ⅱ)可设直线
(Ⅱ)可设直线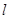 的方程为
的方程为 ,设
,设 ,
, 由
由 得
得 ,
,





 ,故
,故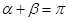
 (Ⅱ)可设直线
(Ⅱ)可设直线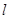 的方程为
的方程为 ,设
,设 ,
, 由
由 得
得 ,
,





 ,故
,故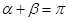
试题分析:(Ⅰ)由已知得:


 ,
, 椭圆C的方程为
椭圆C的方程为
(Ⅱ)由(Ⅰ)知:
 ,
, ,
,

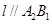


故可设直线
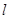 的方程为
的方程为 ,设
,设 ,
,
由
 得
得

 ,即
,即 ,
,

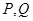 异于椭圆C的顶点,
异于椭圆C的顶点,
 ,
,
 ,
,






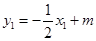 ,
,








又

 ,∴
,∴  ,故
,故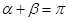 .
.点评:直线与圆锥曲线相交,联立方程利用韦达定理是常用的思路,本题所证明的角的关系转化为直线斜率关系

练习册系列答案
相关题目
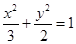 的左、右顶点分别为
的左、右顶点分别为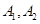 ,点M是椭圆上异于
,点M是椭圆上异于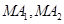 的斜率分别为
的斜率分别为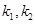 ,求证
,求证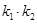 为定值并求出此定值;
为定值并求出此定值;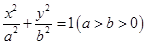 的左、右顶点分别为
的左、右顶点分别为 与椭圆
与椭圆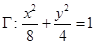 相似,且椭圆
相似,且椭圆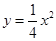 的焦点.
的焦点.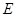 的中心在原点,对称轴在坐标轴上,直线
的中心在原点,对称轴在坐标轴上,直线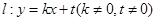 与椭圆
与椭圆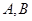 两点,且与椭圆
两点,且与椭圆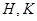 两点.若线段
两点.若线段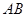 与线段
与线段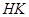 的中点重合,试判断椭圆
的中点重合,试判断椭圆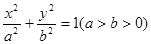 的左右焦点分别为
的左右焦点分别为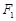 、
、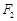 ,短轴两个端点为
,短轴两个端点为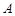 、
、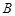 ,且四边形
,且四边形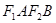 是边长为2的正方形。
是边长为2的正方形。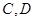 分别是椭圆长轴的左右端点,动点
分别是椭圆长轴的左右端点,动点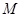 满足
满足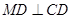 ,连接
,连接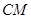 ,交椭圆于点
,交椭圆于点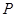 ;证明:
;证明: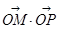 为定值;
为定值; 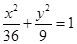 上有两个动点
上有两个动点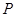 、
、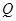 ,
,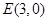 ,
,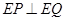 ,则
,则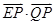 的最小值为( )
的最小值为( )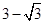
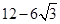
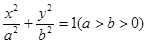 的离心率为
的离心率为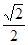 ,且过点
,且过点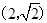 .
.
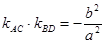 ,
,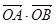 的最值.
的最值.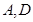 分别是椭圆
分别是椭圆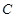 :
: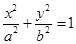 (
(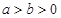 )的左顶点和上顶点,椭圆的左右焦点分别是
)的左顶点和上顶点,椭圆的左右焦点分别是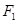 和
和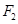 ,点
,点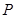 是线段
是线段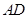 上的动点,如果
上的动点,如果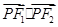 的最大值是
的最大值是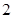 ,最小值是
,最小值是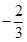 ,那么,椭圆的
,那么,椭圆的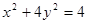 ,直线
,直线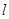 :y=x+m
:y=x+m 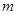 的值;
的值;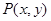 在椭圆
在椭圆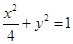 上,则
上,则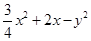 的最大值为( )
的最大值为( )