题目内容
(本题满分14分)
已知椭圆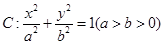 过点
过点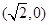 ,且离心率为
,且离心率为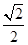 .
.
(1)求椭圆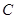 的方程;
的方程;
(2)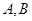 为椭圆
为椭圆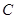 的左右顶点,点
的左右顶点,点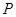 是椭圆
是椭圆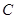 上异于
上异于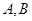 的动点,直线
的动点,直线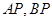 分别交直线
分别交直线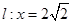 于
于 两点.
两点.
证明:以线段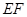 为直径的圆恒过
为直径的圆恒过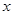 轴上的定点.
轴上的定点.
已知椭圆
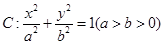 过点
过点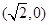 ,且离心率为
,且离心率为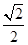 .
.(1)求椭圆
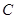 的方程;
的方程;(2)
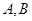 为椭圆
为椭圆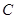 的左右顶点,点
的左右顶点,点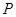 是椭圆
是椭圆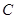 上异于
上异于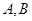 的动点,直线
的动点,直线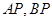 分别交直线
分别交直线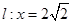 于
于 两点.
两点. 证明:以线段
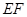 为直径的圆恒过
为直径的圆恒过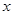 轴上的定点.
轴上的定点.(1) ; (2)
; (2)
 ; (2)
; (2)试题分析:(1)由题意可知,
 , …………1分 而
, …………1分 而 ,……………2分
,……………2分且
 . …………3分 解得
. …………3分 解得 ,……………4分
,……………4分所以,椭圆的方程为
 . ……………5分
. ……………5分(2)由题可得
 .设
.设 , ……………6分
, ……………6分直线
 的方程为
的方程为 , ……………7分
, ……………7分令
 ,则
,则 ,即
,即 ; ……………8分
; ……………8分直线
 的方程为
的方程为 , ……………9分
, ……………9分令
 ,则
,则 ,即
,即 ; ……………10分
; ……………10分证法1:设点
 在以线段
在以线段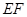 为直径的圆上,则
为直径的圆上,则 ,
, 即
 , …………11分
, …………11分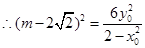 ,而
,而 ,即
,即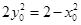 ,
, ,
, 或
或 . ……………13分
. ……………13分故以线段
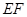 为直径的圆必过
为直径的圆必过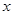 轴上的定点
轴上的定点 、
、 . ……………14分
. ……………14分证法2:以线段
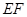 为直径的圆为
为直径的圆为
即
 ………11分
………11分令
 ,得
,得 , ……………12分
, ……………12分而
 ,即
,即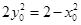 ,
, ,
, 或
或
……………13分
故以线段
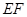 为直径的圆必过
为直径的圆必过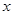 轴上的定点
轴上的定点 、
、 . ……………14分
. ……………14分证法3:令
 ,则
,则 ,令
,令 ,得
,得 ,同理得
,同理得 .
. ∴以
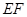 为直径的圆为
为直径的圆为 ,令
,令 解得
解得
∴圆过
 ……………11分
……………11分由前,对任意点
 ,可得
,可得 ,
, 
∴
 ∴
∴ 在以
在以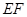 为直径的圆上.
为直径的圆上.同理,可知
 也在
也在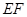 为直径的圆上. ……………13分
为直径的圆上. ……………13分∴故以线段
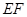 为直径的圆必过
为直径的圆必过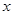 轴上的定点
轴上的定点 、
、 . …………………14分
. …………………14分点评:此题的第二问给出了三种方法来解答,我们要熟练掌握每一种方法。这是作圆锥曲线有关问题的基础。属于中档题。

练习册系列答案
相关题目
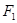
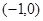 、
、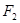
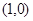 为椭圆的焦点,且直线
为椭圆的焦点,且直线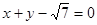 与椭圆相切.
与椭圆相切.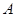 、
、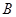 两点,求△
两点,求△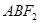 的面积
的面积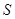 的最大值,并求此时直线的方程。
的最大值,并求此时直线的方程。 与椭圆
与椭圆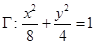 相似,且椭圆
相似,且椭圆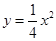 的焦点.
的焦点.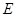 的中心在原点,对称轴在坐标轴上,直线
的中心在原点,对称轴在坐标轴上,直线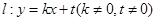 与椭圆
与椭圆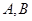 两点,且与椭圆
两点,且与椭圆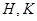 两点.若线段
两点.若线段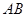 与线段
与线段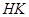 的中点重合,试判断椭圆
的中点重合,试判断椭圆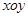 中,椭圆
中,椭圆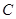 的标准方程为
的标准方程为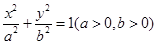 ,右焦点为
,右焦点为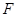 ,右准线为
,右准线为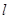 ,短轴的一个端点
,短轴的一个端点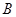 . 设原点到直线
. 设原点到直线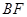 的距离为
的距离为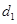 ,
,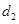 . 若
. 若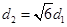 ,则椭圆
,则椭圆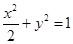 的左焦点
的左焦点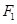 作直线
作直线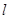 交椭圆于
交椭圆于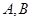 两点,
两点,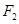 是椭圆右焦点,则
是椭圆右焦点,则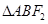 的周长为( )
的周长为( )
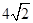


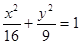 的两焦点是
的两焦点是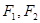 ,则其焦距长为 ,若点
,则其焦距长为 ,若点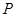 是椭圆上一点,且
是椭圆上一点,且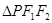 是直角三角形,则
是直角三角形,则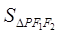 的大小是 .
的大小是 .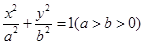 的上顶点坐标为
的上顶点坐标为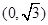 ,离心率为
,离心率为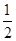 .
.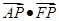 的取值范围.
的取值范围.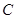 过点
过点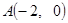 ,且与圆
,且与圆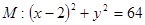 相内切,则动圆
相内切,则动圆 表示焦点在
表示焦点在 轴上的椭圆,则实数
轴上的椭圆,则实数 的取值范围是( )
的取值范围是( )

