Question

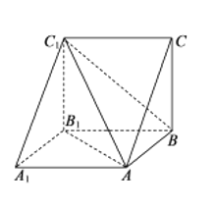
【题目】《九章算术》中记载：将底面为直角三角形的直三棱柱称为堑堵，将一堑堵沿其一顶点与相对的棱剖开，得到一个阳马（底面是长方形，且有一条侧棱与底面垂直的四棱锥）和一个鳖臑（四个面均为直角三角形的四面体）.在如图所示的堑堵中，且有鳖臑C1-ABB1和鳖臑，现将鳖臑沿线BC1翻折，使点C与点B1重合，则鳖臑经翻折后，与鳖臑拼接成的几何体的外接球的表面积是______.

Answer 1

【答案】

【解析】

当沿线BC1翻折，使点C与点B1重合，则鳖臑经翻折后，A点翻折到E点，关于对称，所拼成的几何体为三棱锥，根据外接球的性质及三棱锥性质确定球心，利用勾股定理求出半径即可求解.

当沿线BC1翻折，使点C与点B1重合，则鳖臑经翻折后，A点翻折到E点，关于对称，所拼成的几何体为三棱锥,如图，

由

可得,,

即为正三角形，

所以外接圆圆心为三角形中心，

设三棱锥外接球球心为，连接，则平面，连接,,在中作,垂足为，如图，

因为,,

所以是的中点，由矩形可知,

因为为三角形的中心，

所以

在中，,

所以,

故答案为：