题目内容
15.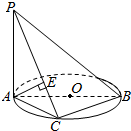 如图所示,已知PA垂直于⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过点A作AE⊥PC于点E,求证:AE⊥PB.
如图所示,已知PA垂直于⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过点A作AE⊥PC于点E,求证:AE⊥PB.
分析 根据底面是圆,得到BC⊥AC,再根据PA⊥平面ABC得到PA⊥BC,最后综合即可证明AE⊥平面PBC,即可证明AE⊥PB.
解答 证明:∵PA⊥平面ABC,∴PA⊥BC.
又∵AB是⊙O的直径,∴BC⊥AC.而PC∩AC=C,∴BC⊥平面PAC.
又∵AE在平面PAC内,∴BC⊥AE.
∵PC⊥AE,且PC∩BC=C,
∴AE⊥平面PBC.
又∵PB?平面PBC,
∴AE⊥PB.
点评 本题考查直线与平面垂直的判定和性质,通过对已知条件的分析,得到线面垂直,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
10.双曲线$\frac{x^2}{3}$-$\frac{y^2}{4}$=1的实轴长、虚轴长、焦点坐标都正确的是( )
| A. | 2a=4,2b=6,F(±5,0) | B. | 2a=6,2b=4,F(±1,0) | ||
| C. | 2a=2$\sqrt{3}$,2b=4,F(0,±5) | D. | 2a=2$\sqrt{3}$,2b=4,F(±$\sqrt{7}$,0) |
20.设点A,B,C为球O的球面上三点,O为球心.球O的表面积为100π,且△ABC是边长为$4\sqrt{3}$的正三角形,则三棱锥O-ABC的体积为( )
| A. | 12 | B. | 12$\sqrt{3}$ | C. | 24$\sqrt{3}$ | D. | 36$\sqrt{3}$ |
7.用辗转相除法求189与161的最大公约数时,需要做的除法的次数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |