题目内容
5.已知数列{an}的前n项和${S_n}={n^2}$,数列{bn}满足b2=2,bn+1=2bn(n∈N*).(1)求数列{an}、{bn}的通项公式;
(2)记数列{anbn}的前n项和为Tn,求Tn<230时的n的最大值.
分析 (1)利用数列的前n项和公式,通过an=Sn-Sn-1求出通项公式;判断数列{bn}是等比数列,求解通项公式即可.
(2)求出数列{anbn}的通项公式,利用错位相减法求出前n项和为Tn,利用表达式求解即可.
解答 解:(1)当n≥2时,${a_n}={S_n}-{S_{n-1}}={n^2}-{(n-1)^2}=2n-1$,…(3分)
又a1=S1=1满足上式,∴an=2n-1、…(5分)
又bn+1=2bn,所以{bn}是公比为2的等比数列,${b_n}={2^{n-1}}$、…(7分)
(2)${T_n}=1•1+3•2+5•{2^2}+…+(2n-1)•{3^{n-1}}①$…(8分)$2{T_n}=1•2+3•{2^2}+5•{2^3}+…+(2n-1)•{3^n}②$…(10分)
①-②得,$-{T_n}=1+2•2+2•{2^2}+…+2•{2^{n-1}}-(2n-1)•{2^n}$=$1+\frac{{4(1-{2^{n-1}})}}{1-2}-(2n-1)•{2^n}=1+{2^{n+1}}-4-(2n-1)•{2^n}=(3-2n)•{2^n}-3$…(13分)
所以${T_n}=(2n-3)•{2^n}+3$、…(14分)
由${T_n}=(2n-3)•{2^n}+3<230$得n≤5,
所以n的最大值为5.…(16分)
点评 本题考查数列的通项公式以及数列的前n项和的求法,不等式的解法,考查转化思想以及计算能力.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
10.某唱片公司计划与参加2015年中国好声音“鸟巢巅峰对决”的张磊、贝贝等5位歌手中的三位签约,这5人被签约的机会均等,则张磊或贝贝被签约的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{10}$ |
17.设经过点 M(2,1)的等轴双曲线的焦点为F1、F2,此双曲线上一点 N满足 NF1⊥NF2,则△NF1F2的面积为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
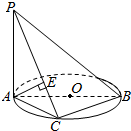 如图所示,已知PA垂直于⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过点A作AE⊥PC于点E,求证:AE⊥PB.
如图所示,已知PA垂直于⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过点A作AE⊥PC于点E,求证:AE⊥PB.