题目内容
3.已知数列{an}的前n项和是Sn,且Sn=-n2+3n,则an=-2n+4.分析 利用递推关系即可得出.
解答 解:∵Sn=-n2+3n,
∴当n=1时,a1=2;
当n≥2时,an=Sn-Sn-1=-n2+3n-[-(n-1)2+3(n-1)]=-2n+4,
当n=1时上式也成立,
则an=-2n+4.
故答案为:-2n+4.
点评 本题考查了递推关系、数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.已知三棱锥S-ABC的底面是以AB为斜边的等腰直角三角形,SA=SB=SC=AB=2,设S,A,B,C四点均在以O为球心的某个球面上,则O到平面ABC的距离为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{2}}{4}$ |
8.下列函数中,是偶函数的是( )
| A. | f(x)=x | B. | f(x)=|x| | C. | f(x)=x3 | D. | f(x)=$\frac{1}{x}$ |
12.函数y=$\sqrt{4-3x-{x^2}}$的单调递增区间是( )
| A. | $({-∞,-\frac{3}{2}}]$ | B. | $[{-\frac{3}{2},+∞})$ | C. | $[{-4,-\frac{3}{2}}]$ | D. | $[{-\frac{3}{2},1}]$ |
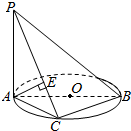 如图所示,已知PA垂直于⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过点A作AE⊥PC于点E,求证:AE⊥PB.
如图所示,已知PA垂直于⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过点A作AE⊥PC于点E,求证:AE⊥PB.