题目内容
6.(1)解关于x的不等式:$\frac{ax-1}{x-1}>a$;(2)记(1)中不等式的解集为 A,若 A⊆R+,证明:2a3+4a≥5a2+1.
分析 (1)$\frac{ax-1}{x-1}>a$化为:(a-1)(x-1)>0,对a分类讨论即可得出;
(2)由于A⊆R+,因此取A=[1,+∞).则a≥1,作差2a3+4a-(5a2+1)=(2a-1)(a-1)2,即可证明.
解答 (1)解:$\frac{ax-1}{x-1}>a$化为:(a-1)(x-1)>0,当a>1时,不等式的解集为(1,+∞);
当a=1时,不等式的解集为∅;
当a<1时,不等式的解集为(-∞,1).
(2)证明:∵A⊆R+,
∴取A=[1,+∞).
即a≥1,
∴2a3+4a-(5a2+1)=(2a-1)(a-1)2≥0.
∴2a3+4a≥5a2+1.
点评 本题考查了分式不等式的解法、“作差法”、不等式的性质,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
17.设经过点 M(2,1)的等轴双曲线的焦点为F1、F2,此双曲线上一点 N满足 NF1⊥NF2,则△NF1F2的面积为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
1.已知集合A={-1,0,1,2,3},B={x|(x+1)(x-3)<0},则A∩B=( )
| A. | {-1,3} | B. | {0,1} | C. | {0,1,2} | D. | {1,2,3} |
18.已知三棱锥S-ABC的底面是以AB为斜边的等腰直角三角形,SA=SB=SC=AB=2,设S,A,B,C四点均在以O为球心的某个球面上,则O到平面ABC的距离为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{2}}{4}$ |
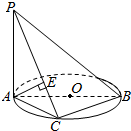 如图所示,已知PA垂直于⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过点A作AE⊥PC于点E,求证:AE⊥PB.
如图所示,已知PA垂直于⊙O所在的平面,AB是⊙O的直径,C是⊙O上任意一点,过点A作AE⊥PC于点E,求证:AE⊥PB.