题目内容
17.在正三角形ABC的底边BC上取中点M,在与底边BC相邻的两条边BA和CA上分别取点P、Q,若线段PQ对M的张角∠PMQ为锐角,则称点P、Q亲密.若点P、Q在BA、CA上的位置随机均匀分布,则P、Q亲密的概率称为正三角形的亲密度.则正三角形的亲密度为$\frac{6-3ln3}{4}$.分析 设AB=BC=CA=2,设BP=x,0≤x≤2,过M作PM的垂线,交AC于R,当Q落在线段AR内部及A点上时,P与Q是亲密的,记AR的长度为y=f(x),由PM2+MR2=RP2及余弦定理得y=$\frac{3x}{1+x}$,由此利用定积分能求出正三角形的亲密度.
解答 解: 设AB=BC=CA=2,设BP=x,0≤x≤2,
设AB=BC=CA=2,设BP=x,0≤x≤2,
过M作PM的垂线,交AC于R,当Q落在线段AR内部及A点上时,P与Q是亲密的,
记AR的长度为y=f(x),
由PM2+MR2=RP2及余弦定理得:
(x2-x+1)+[(2-y)2+(2-y)+1]=(2-x)2-(2-x)y+y2,
整理,得:y=$\frac{3x}{1+x}$,
∴正三角形的亲密度为:
$\frac{1}{4}{∫}_{0}^{2}\frac{3x}{1+x}dx$=$\frac{3}{4}$${∫}_{0}^{2}\frac{x}{1+x}dx$=$\frac{3}{4}$[${∫}_{0}^{2}(1-\frac{1}{1+x})dx$]=$\frac{3}{4}$[x-ln(x+1)]${|}_{0}^{2}$=$\frac{6-3ln3}{4}$.
故答案为:$\frac{6-3ln3}{4}$.
点评 本题考查正三角形的亲密度的求法,涉及到正三角形性质、函数、定积分等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想,考查创新意识、应用意识,是中档题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
19.函数f(x)=$\sqrt{x+1}$+lg(6-3x)的定义域为( )
| A. | (-∞,2) | B. | (2,+∞) | C. | [-1,2) | D. | [-1,2] |
20.半径为2的球内有一底面边长为2的内接正四棱柱(底面是正方形,侧棱垂直底面),则当该正四棱柱的侧面积最大时球的表面积与该正四棱柱的侧面积之差是( )
| A. | $16({π-\sqrt{3}})$ | B. | $16({π-\sqrt{2}})$ | C. | $8({2π-3\sqrt{2}})$ | D. | $8({2π-\sqrt{3}})$ |
7.在四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{DC}$=(2,0),$\frac{\overrightarrow{BA}}{|\overrightarrow{BA}|}$+$\frac{\overrightarrow{BC}}{|\overrightarrow{BC}|}$=$\frac{\overrightarrow{BD}}{|\overrightarrow{BD}|}$,则四边形ABCD的面积是( )
| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{2}$ |
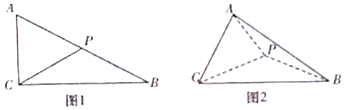 如图1,在△ABC中,AC=2,∠ACB=90°,∠ABC=30°,P是AB边的中点,现把△ACP沿CP折成如图2所示的三棱锥A-BCP,使得AB=$\sqrt{10}$.
如图1,在△ABC中,AC=2,∠ACB=90°,∠ABC=30°,P是AB边的中点,现把△ACP沿CP折成如图2所示的三棱锥A-BCP,使得AB=$\sqrt{10}$.