题目内容
下列函数中与函数y=-3|x|奇偶性相同且在（-∞，0）上单调性也相同的是（ ）
A、y=-
| ||
| B、y=log2|x| | ||
| C、y=1-x2 | ||
| D、y=x3-1 |
考点：函数单调性的判断与证明,函数奇偶性的判断
专题：函数的性质及应用
分析：先判定函数y=-3|x|的奇偶性以及在（-∞，0）上的单调性，再对选项A、B、C、D中的函数逐一判定，找出复合条件的函数．
解答：
解：∵函数y=-3|x|是偶函数，且在（-∞，0）上是减函数，
∴对于A，y=-
是奇函数，不满足条件；
对于B，y=log2|x|是偶函数，在（-∞，0）上是增函数，∴不满足条件；
对于C，y=1-x2是偶函数，且在（-∞，0）上是减函数，∴满足条件；
对于D，y=x3-1是非奇非偶的函数，∴不满足条件．
故选：C．
∴对于A，y=-
| 1 |
| x |
对于B，y=log2|x|是偶函数，在（-∞，0）上是增函数，∴不满足条件；
对于C，y=1-x2是偶函数，且在（-∞，0）上是减函数，∴满足条件；
对于D，y=x3-1是非奇非偶的函数，∴不满足条件．
故选：C．
点评：本题考查了函数的奇偶性与单调性问题，解题时应对每一个选项中的函数进行判定，从而得出正确的结论，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若向量
=（x-2，3）与向量
=（1，y+2）相等，则（ ）
| a |
| b |
| A、x=1，y=3 |
| B、x=3，y=1 |
| C、x=1，y=-5 |
| D、x=5，y=-1 |
函数f（x）=
（0≤x≤2π）的值域为（ ）
| sinx-1 | ||
|
| A、[-1，0] | ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
执行如图所示的程序框图，如果输入a=2，b=2，那么输出的a值为（ ）| A、log316 |
| B、256 |
| C、16 |
| D、4 |
给出下面四个命题，其中正确的一个是（ ）
A、回归直线
| ||||||
| B、在线性回归模型中，相关指数R2=0.64，说明预报变量对解释变量个贡献率是64% | ||||||
| C、相关指数R2用来刻画回归效果，R2越小，则残差平方的和越大，模型的拟合效果越好 | ||||||
| D、随机误差e是引起预报值与真实值之间存在误差的原因之一 |
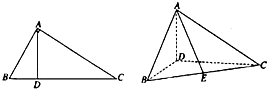如图，在△ABC中，AB⊥AC，AD⊥BC，∠ABC=