题目内容
函数y=4x-
x3的单调递增区是( )
| 1 |
| 3 |
分析:先求函数y=4x-
x3的导函数y′,然后令y′>0,解之即可求出函数的单调增区间.
| 1 |
| 3 |
解答:解:∵y=4x-
x3,
∴y′=4-x2,
令y′=4-x2>0,解得-2<x<2,
∴函数y=4x-
x3的单调递增区是(-2,2).
故选D.
| 1 |
| 3 |
∴y′=4-x2,
令y′=4-x2>0,解得-2<x<2,
∴函数y=4x-
| 1 |
| 3 |
故选D.
点评:本题考查了利用导数研究函数的单调,对于利用导数研究函数的单调性,注意导数的正负对应着函数的单调性.利用导数研究函数问题时,经常会运用分类讨论的数学思想方法.属于中档题.

练习册系列答案
相关题目
设变量x,y满足约束条件
,则目标函数z=4x+y的最大值为( )
|
| A、4 | B、11 | C、12 | D、14 |
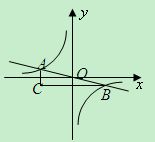 如图,反比例函数
如图,反比例函数