题目内容
已知不共线向量 则
则
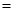
A. | B. | C. | D. |
A
解析试题分析:因为 ,所以
,所以 ,
,
故

 .
.
考点:向量的数量积
点评:本题主要考查向量的数量积运与向量数量积的运算律,以及考查数量积的性质与数量积的应用如①求模;②求夹角;③判直线垂直,本题考查求夹角,属于基础题.

练习册系列答案
相关题目
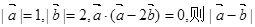 = ( )
= ( )
| A.2 | B.4 | C.1 | D.8 |
在R t △PAB中,PA=PB,点C、D分别在PA、PB上,且CD∥AB,AB=3,AC= ,则
,则 的值为( )
的值为( )
| A.-7 | B.0 | C.-3 | D.3 |
设 、
、 、
、 为同平面内具有相同起点的任意三个非零向量,且满足
为同平面内具有相同起点的任意三个非零向量,且满足 与
与 不共线,
不共线, ,
, ,则
,则 的值一定等于( )
的值一定等于( )
A.以 、 、 为两边的三角形面积; 为两边的三角形面积; | B.以 、 、 为邻边的平行四边形的面积; 为邻边的平行四边形的面积; |
C.以 、 、 为两边的三角形面积; 为两边的三角形面积; | D.以 、 、 为邻边的平行四边形的面积. 为邻边的平行四边形的面积. |
在△ABC中,D为BC边上的点, =
=
 +
+
 ,则
,则 的最大值为
的最大值为
| A.1 | B. | C. | D. |
 是边长为
是边长为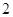 的正三角形,则
的正三角形,则 =( )
=( )
A. | B. | C.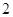 | D. |
在 中,
中,  ,
, 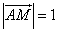 ,点
,点 在
在 上且满足
上且满足 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
已知向量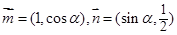 ,且
,且 ,则
,则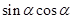 等于
等于
A. | B.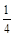 | C. | D. |
 ,
, ,对任意
,对任意 ,恒有
,恒有 ,则( )
,则( ) B.
B. C.
C. D.
D. 