题目内容
在 中,
中,  ,
, 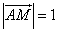 ,点
,点 在
在 上且满足
上且满足 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
D
解析试题分析:∵ ,∴M为BC的中点,∴
,∴M为BC的中点,∴ ,∴
,∴ ,又
,又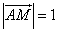 ,∴
,∴ ,∴
,∴ 等于
等于 ,故选D
,故选D
考点:本题考查了向量的运算
点评:掌握向量的运算及数量积的定义是解决此类问题的关键,属基础题

练习册系列答案
相关题目
若非零向量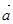 ,
, 满足
满足 ,且
,且 ,则向量
,则向量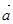 ,
, 的夹角为 ( )
的夹角为 ( )
A.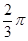 | B. | C. | D. |
已知不共线向量 则
则
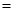
A. | B. | C. | D. |
若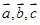 均为单位向量,且
均为单位向量,且 ,则
,则 的最大值为( )
的最大值为( )
| A.3 | B. | C.1 | D. +1 +1 |
已知△ABC, , 则△ABC的面积为( )
, 则△ABC的面积为( )
| A.1 | B.2 | C.3 | D.4 |
设 R,向量
R,向量 ,且
,且 ,则
,则 ( )
( )
A.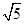 | B. | C. | D.10 |
平面向量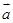 与
与 的夹角为
的夹角为 ,
,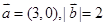 ,则
,则 = ( )
= ( )
| A.7 | B. | C. | D.3 |
已知
A. | B. | C. | D. |
在空间直角坐标系中,若向量 ,则它们之间的关系是( )
,则它们之间的关系是( )
A. | B.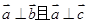 | C. | D. |